决策论decision theory

用于分析决策问题（主要指不完全信息下的决策问题）的概念、准则、程序和方法，也称决策分析。
决策是为实现特定目标，在占有一定信息的基础上，对若干备选方案进行科学分析后选取其中一种方案的活动。自古以来，决策者主要凭借个人的经验、知识和才能进行决策。随着控制论、运筹学、电子计算机等的发展，逐步使决策建立在科学的基础上。
1931年拉姆赛(F.P.Ramsey)首先提出了基于主观概率和效用的决策理论。1944年冯·诺伊曼(J.von Neumann)和摩根斯特恩(O.Morgenstern)提出了决策效用理论。60年代统计决策理论日益广泛应用，西蒙(H.A.Simon)等人对决策理论作出了重要贡献。
决策模型的基本结构 决策模型的基本结构是U=f(a_i,S_j)。式中U为支付值；a_i为备选方案；S_j为自然状态。
单一目标的决策问题可用决策表表示如下。

决策表的一般结构

自然状态 概率 备选方案	S1	S2	…	Sm
	P1	P2	…	Pm
a1 a2	U11 U21	U12 U22	… …	U1m U2m
⋮	⋮	⋮		⋮
an	Un1	Un2	…	Unm

表中包括备选方案a_i、自然状态S_j、自然状态的概率P_j和支付值U_j四项要素。备选方案是决策者可以控制的因素，称为决策变量。自然状态是不可控变量。可以是经济状况、天气情况或决策者不能控制的其他环境条件。自然状态概率也是不可控变量。各自然状态的概率之和必等于1。支付值U_ij是结果变量，表示第i种方案在第j种自然状态下的支付值。它们可用货币量或其他物理量，如天数、小时数等计量，还可用效用值表示。效用值是决策者对决策后果偏好的尺度。效用值由效用函数给出。决策者偏好决定了效用函数的类型。例如，对于一个敢冒风险的决策者，他对获利较大但风险也较大的策略给予较大的效用值，而对获利较小，但比较有把握的策略给予较小的效用值。其效用函数是凹的。对于一个持稳重态度的决策者来说，则常常采取比较稳妥的策略，提高获利较小而把握较大的策略的效用值，降低获利较大但风险也较大的策略的效用值，其效用函数是凸的。
对于多层次的决策过程，可用决策树表示。其结构如下图。图中□为决策点，○为机会点，——为支。S₁为旱年、P₁为出现旱年的概率；S₂为正常年，P₂为出现正常年的概率；S₃为涝年，P₃为出现涝年的概率。

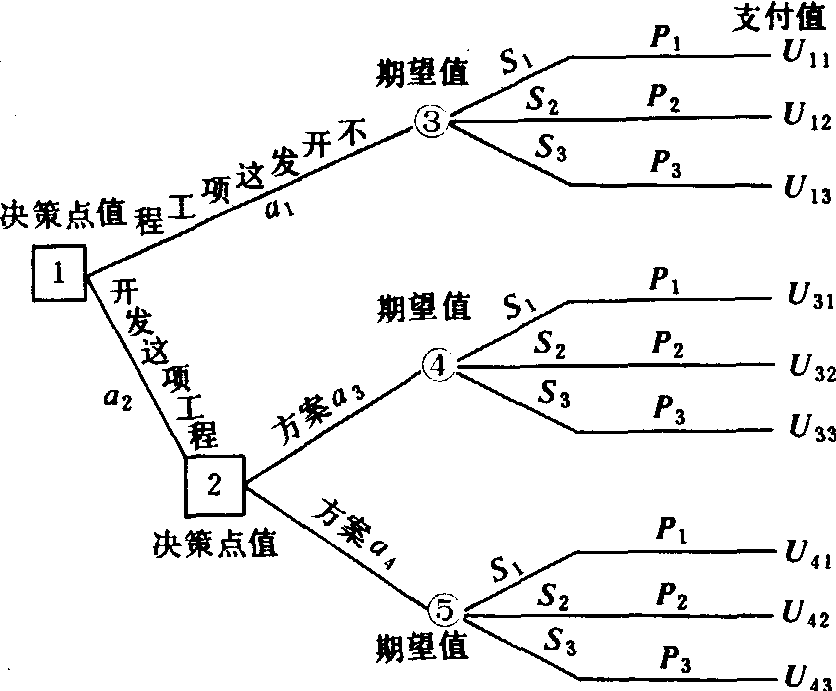
某地区农田基本建设工程决策树图

决策问题的类型 根据决策者掌握信息情况的不同，可以把决策问题分为三种类型：确定型、不确定型和风险型。
确定型决策 在充分掌握有关信息的情况下进行的决策。对于确定型决策来说，只有一种自然状态，其概率等于1。
不确定型决策 决策者未掌握自然状态概率情况下进行的决策。在不确定型决策中，采取的决策准则有五种。❶等概率准则：假定所有的自然状态出现的概率相等。用公式表示为：。
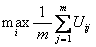❷悲观的准则：以假定将发生最不利情况作为选择方案的准则，用公式表示为：。
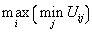❸乐观的准则：以假定将发生最好情况作为选择方案的准则。用公式表示为：。
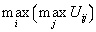❹折中的准则：假定将发生的情况不是最好的，也不是最差的。用公式表示为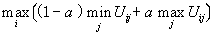：，式中α为乐观系数，0<α<1。
❺机会损失准则： 机会损失是指由于没有选择最好的方案而可能损失的支付值。按这种准则进行决策， 首先计算每种方案在每种自然状态下的机会损失值，找出每种方案的机会损失最大值，再从中选择其最小值的方案作为决策方案。用公式表示为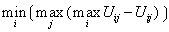：。实际上，根据不同的决策准则所得的结果可能是不同的。决策者可以根据具体情况作出最后的选择。
风险型决策 决策者掌握不完全信息的情况下进行的决策。决策者必须在考虑几种可能发生的自然状态及其概率的情况下作出决策，因而带有一定的风险。这是最常见的决策状态。在风险型决策中，通常采用期望值准则选择最优方案。在目标最大化时，在所有方案中选择期望值Ei最大的方案为决策方案。用公式表示为：

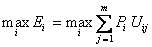
解决风险型决策的关键是估计自然状态的概率。为此，❶决策者先初步提出一个自然状态概率的估计值，称为先验概率。
❷通过试验或调查研究取得有关自然状态的附加信息。
❸利用获得的附加信息修改先验概率，称为后验概率。上述方法称为贝叶斯分析。应注意：仅当调查或试验所获效益大于费用时此法才有应用价值。
序贯决策 按照同一目标相继采取一系列的决策活动以实现总体优化的决策过程。解决这类问题通常采用动态规划法（见数学规划）。序贯决策有确定型和风险型两种，后者也称为随机序贯决策，解决随机序贯决策时涉及马尔科夫过程。系统从一种状态向另一种状态转移的概率称为转移概率。如果此转移概率只取决于现在的状态而与以往的经历无关，则这种变化过程称为马尔科夫过程。
例如某地区的天气可分为晴、阴、雨三种情况。设用S₁、S₂、S₃分别表示这三种天气的状态，则这三种天气相互转移的情况可用转移概率矩阵P表达如下：

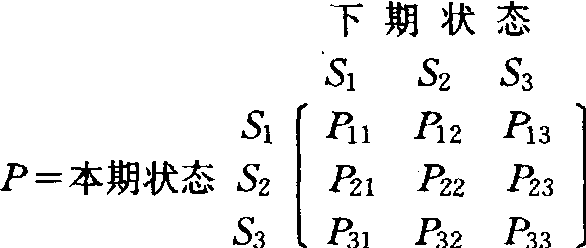
设初始状态的概率向量为π⁽⁰⁾，本期状态的概率向量为π⁽ⁿ⁾，下期状态的概率向量为π⁽ⁿ⁺¹⁾，则马尔科夫状态转移方程为：

式中 m为独立状态数，n为状态转移期数。当n无限增大时，则状态概率向量趋于稳定，这时的概率称为均衡状态概率。
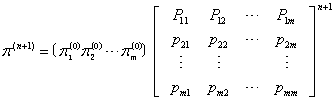
马尔可夫过程决策 把不同的行动策略与其相应均衡状态的概率联系起来，计算采取不同策略可得的经济效益，从中选择最佳方案的决策方法。