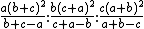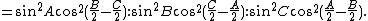- Definition
- Trilinear coordinates
- References
- See also
In triangle geometry, the Apollonius point is a special point associated with a plane triangle. The point is a triangle center and it is designated as X(181) in Clark Kimberling's Encyclopedia of Triangle Centers (ETC).
The Apollonius center is also related to the Apollonius problem.
In the literature, the term "Apollonius points" has also been used to refer to the isodynamic points of a triangle.[1] This usage could also be justified on the ground that the isodynamic points are related to the three Apollonian circles associated with a triangle.
The solution of the Apollonius problem has been known for centuries. But the Apollonius point was first noted in 1987.[2][3]
Definition
The Apollonius point of a triangle is defined as follows.
Let ABC be any given triangle. Let the excircles of triangle ABC opposite to the vertices A, B, C be EA, EB, EC respectively. Let E be the circle which touches the three excircles EA, EB, EC such that the three excircles are within E. Let A' , B' , C' be the points of contact of the circle E with the three excircles. The lines AA' , BB' , CC' are concurrent. The point of concurrence is the Apollonius point of triangle ABC.
The Apollonius problem is the problem of constructing a circle tangent to three given circles in a plane. In general, there are eight circles touching three given circles. The circle E referred to in the above definition is one of these eight circles touching the three excircles of triangle ABC. In Encyclopedia of Triangle Centers the circle E is the called the Apollonius circle of triangle ABC.
Trilinear coordinates
The trilinear coordinates of the Apollonius point are[2]
References
2. ^1 {{cite web|last=Kimberling |first=Clark |title=Apollonius Point |url=http://faculty.evansville.edu/ck6/tcenters/recent/apollon.html |accessdate=16 May 2012 |deadurl=yes |archiveurl=https://web.archive.org/web/20120510142037/http://faculty.evansville.edu/ck6/tcenters/recent/apollon.html |archivedate=10 May 2012 }}
3. ^{{cite journal|last=C. Kimberling|author2=Shiko Iwata |author3=Hidetosi Fukagawa |title=Problem 1091 and Solution|journal=Crux Mathematicorum|year=1987|volume=13|pages=217–218}}
See also
- Apollonius' theorem
- Apollonius of Perga (262–190 BC), geometer and astronomer
- Apollonius problem
- Apollonian circles
- Isodynamic point of a triangle
- Work in Progress (1951 film)
- Work in Progress (2000 film)
- Work in Progress (Man Alive album)
- Work In Progress Productions
- Work in Progress (song)
- Workin' Them Angels
- Work Is a Four-Letter Word
- Work it baby
- Work It Baby
- Work It (disambiguation)
- Work It Out (album)
- Work It Out (Beyonce Knowles song)
- Work It Out (disambiguation)
- Work It Out/In the House
- Work it Out (Jurassic 5 song)
- Work It Out (Q-Tip song)
- Work It Out (Steve "Silk" Hurley song)
- Work It Out with Chet Atkins C.G.P.
- Workitu Ayanu Gurmu
- WORK-IX
- Work kinetic energy theorem
- Work-kinetic energy theorem
- Worklecy
- WorkLenz
- Work-Less Party