1. Definition

2. Types of arrangement

3. Applications

4. References

In discrete geometry, an arrangement is the decomposition of the d-dimensional linear, affine, or projective space into connected cells of different dimensions, induced by a finite collection of geometric objects, which are usually of dimension one less than the dimension of the space, and often of the same type as each other, such as hyperplanes or spheres.

Definition

For a set of objects in , the cells in the arrangement

are the connected components of sets of the form

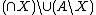
for subsets of . That is, for each the cells are the connected components of the points that belong to every object in and do not belong to any other object. For instance the cells of an arrangement of lines in the Euclidean plane are of three types:

• Isolated points, for which is the subset of all lines that pass through the point.
• Line segments or rays, for which is a singleton set of one line. The segment or ray is a connected component of the points that belong only to that line and not to any other line of
• Convex polygons (possibly unbounded), for which is the empty set, and its intersection (the empty intersection) is the whole space. These polygons are the connected components of the subset of the plane formed by removing all the lines in .

Types of arrangement

Of particular interest are the arrangements of lines and arrangements of hyperplanes.

More generally, geometers have studied arrangements of other types of curves in the plane, and of other more complicated types of surface.^[1] Arrangements in complex vector spaces have also been studied; since complex lines do not partition the complex plane into multiple connected components, the combinatorics of vertices, edges, and cells does not apply to these types of space, but it is still of interest to study their symmetries and topological properties.^[2]

Applications

An interest in the study of arrangements was driven by advances in computational geometry, where the arrangements were unifying structures for many problems. Advances in study of more complicated objects, such as algebraic surfaces, contributed to "real-world" applications, such as motion planning and computer vision.^[3]

References

• Curacoi
• Curacoites
• Curacoites rotundus
• Curacó Department
• Cura del Popolo
• Cura (genus)
• Curah!
• Curalium cronini
• Curama language
• Curam Duo
• Curanave language
• Curantyl
• Cura pinguis
• Curare poisoning
• Cura sa carsije
• Cura saz
• Cura sa čaršije
• Cura Si Manjakini
• Curatari
• Cura te ipsum
• Curatesti
• Curatin
• Curating
• Curative
• Curative mud