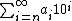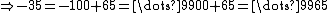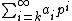- Introduction
- p-adic expansions
- Notation
- Constructions Analytic approach Algebraic approach
- Properties Cardinality Topology Metric completions and algebraic closures Multiplicative group of {{math|Qp}} Analysis on {{math|Qp}}
- Rational arithmetic
- Generalizations and related concepts
- Local–global principle
- See also
- Footnotes Notes Citations
- References
- Further reading
- External links
In mathematics, the {{mvar|p}}-adic number system for any prime number {{mvar|p}} extends the ordinary arithmetic of the rational numbers in a different way from the extension of the rational number system to the real and complex number systems. The extension is achieved by an alternative interpretation of the concept of "closeness" or absolute value. In particular, {{mvar|p}}-adic numbers are considered to be close when their difference is divisible by a high power of {{mvar|p}}: the higher the power, the closer they are. This property enables {{mvar|p}}-adic numbers to encode congruence information in a way that turns out to have powerful applications in number theory – including, for example, in the famous proof of Fermat's Last Theorem by Andrew Wiles.[1]
{{mvar|p}}-adic numbers were first described by Kurt Hensel in 1897,[2] though, with hindsight, some of Ernst Kummer's earlier work can be interpreted as implicitly using {{mvar|p}}-adic numbers.[3] The {{mvar|p}}-adic numbers were motivated primarily by an attempt to bring the ideas and techniques of power series methods into number theory. Their influence now extends far beyond this. For example, the field of {{mvar|p}}-adic analysis essentially provides an alternative form of calculus.More formally, for a given prime {{mvar|p}}, the field {{math|Qp}} of {{mvar|p}}-adic numbers is a completion of the rational numbers. The field {{math|Qp}} is also given a topology derived from a metric, which is itself derived from the {{math|p}}-adic order, an alternative valuation on the rational numbers. This metric space is complete in the sense that every Cauchy sequence converges to a point in {{math|Qp}}. This is what allows the development of calculus on {{math|Qp}}, and it is the interaction of this analytic and algebraic structure that gives the {{mvar|p}}-adic number systems their power and utility.
The {{mvar|p}} in "{{mvar|p}}-adic" is a variable and may be replaced with a prime (yielding, for instance, "the 2-adic numbers") or another placeholder variable (for expressions such as "the ℓ-adic numbers"). The "adic" of "{{mvar|p}}-adic" comes from the ending found in words such as dyadic or triadic.
Introduction
This section is an informal introduction to {{math|p}}-adic numbers, using examples from the ring of 10-adic (decadic) numbers. Although for {{math|p}}-adic numbers {{math|p}} should be a prime, base 10 was chosen to highlight the analogy with decimals. The decadic numbers are generally not used in mathematics: since 10 is not prime or prime power, the decadics are not a field. More formal constructions and properties are given below.
In the standard decimal representation, almost all[4] real numbers do not have a terminating decimal representation. For example, 1/3 is represented as a non-terminating decimal as follows
Informally, non-terminating decimals are easily understood, because it is clear that a real number can be approximated to any required degree of precision by a terminating decimal. If two decimal expansions differ only after the 10th decimal place, they are quite close to one another; and if they differ only after the 20th decimal place, they are even closer.
10-adic numbers use a similar non-terminating expansion, but with a different concept of "closeness". Whereas two decimal expansions are close to one another if their difference is a large negative power of 10, two 10-adic expansions are close if their difference is a large positive power of 10. Thus 4739 and 5739, which differ by 103, are close in the 10-adic world, and 72694473 and 82694473 are even closer, differing by 107.
More precisely, a positive rational number {{mvar|r}} can be uniquely expressed as {{math|r =: {{sfrac|p|q}}·10d}}, where {{mvar|p}}, {{mvar|q}} and 10 are positive integers and are all relatively prime with respect to each other. Let the {{nowrap|10-adic}} "absolute value"[5] of {{mvar|r}} be
.
Additionally, we define
.
Now, taking {{math|p/q = 1}} and {{math|d = 0,1,2,...}} we have
{{math||100|10 = 100}}, {{math||101|10 = 10−1}}, {{math||102|10 = 10−2, ...}},
with the consequence that we have
.
Closeness in any number system is defined by a metric. Using the 10-adic metric the distance between numbers {{mvar|x}} and {{mvar|y}} is given by {{math||{{mvar|x}} − {{mvar|y}}|10}}. An interesting consequence of the 10-adic metric (or of a {{mvar|p}}-adic metric) is that there is no longer a need for the negative sign. (In fact, there is no order relation which is compatible with the ring operations and this metric) As an example, by examining the following sequence we can see how unsigned 10-adics can get progressively closer and closer to the number −1:
so
.
so
.
so
.
so
.
and taking this sequence to its limit, we can deduce the 10-adic expansion of −1
,
thus
,
an expansion which clearly is a ten's complement representation.
In this notation, 10-adic expansions can be extended indefinitely to the left, in contrast to decimal expansions, which can be extended indefinitely to the right. Note that this is not the only way to write {{mvar|p}}-adic numbers – for alternatives see the Notation section below.
More formally, a 10-adic number can be defined as
where each of the {{math|ai}} is a digit taken from the set {0, 1, … , 9} and the initial index {{mvar|n}} may be positive, negative or 0, but must be finite. From this definition, it is clear that positive integers and positive rational numbers with terminating decimal expansions will have terminating 10-adic expansions that are identical to their decimal expansions. Other numbers may have non-terminating 10-adic expansions.
It is possible to define addition, subtraction, and multiplication on 10-adic numbers in a consistent way, so that the 10-adic numbers form a commutative ring.
We can create 10-adic expansions for "negative numbers"[6] as follows
and fractions which have non-terminating decimal expansions also have non-terminating 10-adic expansions. For example
Generalizing the last example, we can find a 10-adic expansion with no digits to the right of the decimal point for any rational number {{math|p/q}} such that {{math|q}} is co-prime to 10; Euler's theorem guarantees that if {{mvar|q}} is co-prime to 10, then there is an {{mvar|n}} such that {{math|10n − 1}} is a multiple of {{math|q}}. The other rational numbers can be expressed as 10-adic numbers with some digits after the decimal point.
As noted above, 10-adic numbers have a major drawback. {{anchor|zero_div}}It is possible to find pairs of non-zero 10-adic numbers (which are not rational, thus having an infinite number of digits) whose product is 0.[7][8] This means that 10-adic numbers do not always have multiplicative inverses i.e. valid reciprocals, which in turn implies that though 10-adic numbers form a ring they do not form a field, a deficiency that makes them much less useful as an analytical tool. Another way of saying this is that the ring of 10-adic numbers is not an integral domain because they contain zero divisors.[8] The reason for this property turns out to be that 10 is a composite number which is not a power of a prime. This problem is simply avoided by using a prime number {{mvar|p}} or a prime power {{mvar|pn}} as the base of the number system instead of 10 and indeed for this reason {{mvar|p}} in {{mvar|p}}-adic is usually taken to be prime.
| fraction | original decimal notation | 10-adic notation | fraction | original decimal notation | 10-adic notation | fraction | original decimal notation | 10-adic notation |
 | 0.5 | 0.5 |  | 714285}} | 428571}}5 |  | 0.9 | 0.9 |
 | 3}} | 6}}7 |  | 857142}} | 714285}}8 |  | 09}} | 09}}1 |
 | 6}} | 3}}4 |  | 0.125 | 0.125 |  | 18}} | 18}}2 |
 | 0.25 | 0.25 |  | 0.375 | 0.375 |  | 27}} | 27}}3 |
 | 0.75 | 0.75 |  | 0.625 | 0.625 |  | 36}} | 36}}4 |
 | 0.2 | 0.2 |  | 0.875 | 0.875 |  | 45}} | 45}}5 |
 | 0.4 | 0.4 |  | 1}} | 8}}9 | 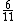 | 54}} | 54}}6 |
 | 0.6 | 0.6 |  | 2}} | 7}}8 |  | 63}} | 63}}7 |
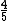 | 0.8 | 0.8 |  | 4}} | 5}}6 |  | 72}} | 72}}8 |
 | 6}} | 3}}.5 |  | 5}} | 4}}5 |  | 81}} | 81}}9 |
 | 3}} | 6}}7.5 |  | 7}} | 2}}3 |  | 90}} | 09}}10 |
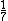 | 142857}} | 285714}}3 |  | 8}} | 1}}2 |  | 3}} | 6}}.75 |
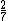 | 285714}} | 571428}}6 |  | 0.1 | 0.1 |  | 6}} | 3}}.75 |
 | 428571}} | 857142}}9 |  | 0.3 | 0.3 |  | 3}} | 6}}7.25 |
 | 571428}} | 142857}}2 |  | 0.7 | 0.7 |  | 6}} | 3}}4.25 |
p-adic expansions
{{needs more references|date=February 2019}}When dealing with natural numbers, if we take {{mvar|p}} to be a fixed prime number, then any positive integer can be written as a base {{mvar|p}} expansion in the form
where the ai are integers in {0, … , {{math|p − 1}}}.[9] For example, the binary expansion of 35 is 1·25 + 0·24 + 0·23 + 0·22 + 1·21 + 1·20, often written in the shorthand notation 1000112.
The familiar approach to extending this description to the larger domain of the rationals[10][11] (and, ultimately, to the reals) is to use sums of the form:
A definite meaning is given to these sums based on Cauchy sequences, using the absolute value as metric. Thus, for example, 1/3 can be expressed in base 5 as the limit of the sequence 0.1313131313...5. In this formulation, the integers are precisely those numbers for which ai = 0 for all i < 0.
With p-adic numbers, on the other hand, we choose to extend the base {{mvar|p}} expansions in a different way. Unlike traditional integers, where the magnitude is determined by how far they are from zero, the "size" of {{mvar|p}}-adic numbers is determined by the {{mvar|p}}-adic absolute value, where high positive powers of {{mvar|p}} are relatively small compared to high negative powers of {{mvar|p}}. Consider infinite sums of the form:
where k is some (not necessarily positive) integer, and each coefficient  can be called a {{mvar|p}}-adic digit.[12] With this approach we obtain the {{mvar|p}}-adic expansions of the {{mvar|p}}-adic numbers. Those {{mvar|p}}-adic numbers for which ai = 0 for all i < 0 are also called the {{mvar|p}}-adic integers.
can be called a {{mvar|p}}-adic digit.[12] With this approach we obtain the {{mvar|p}}-adic expansions of the {{mvar|p}}-adic numbers. Those {{mvar|p}}-adic numbers for which ai = 0 for all i < 0 are also called the {{mvar|p}}-adic integers.
As opposed to real number expansions which extend to the right as sums of ever smaller, increasingly negative powers of the base {{mvar|p}}, {{mvar|p}}-adic numbers may expand to the left forever, a property that can often be true for the {{mvar|p}}-adic integers. For example, consider the {{mvar|p}}-adic expansion of 1/3 in base 5. It can be shown to be …1313132{{sub|5}}, i.e., the limit of the sequence 2{{sub|5}}, 32{{sub|5}}, 132{{sub|5}}, 3132{{sub|5}}, 13132{{sub|5}}, 313132{{sub|5}}, 1313132{{sub|5}}, … :
Multiplying this infinite sum by 3 in base 5 gives …0000001{{sub|5}}. As there are no negative powers of 5 in this expansion of 1/3 (i.e. no numbers to the right of the decimal point), we see that 1/3 satisfies the definition of being a {{mvar|p}}-adic integer in base 5.
More formally, the {{mvar|p}}-adic expansions can be used to define the field {{math|Qp}} of {{mvar|p}}-adic numbers while the {{mvar|p}}-adic integers form a subring of {{math|Qp}}, denoted {{math|Zp}}. (Not to be confused with the ring of integers modulo {{mvar|p}} which is also sometimes written {{math|Zp}}. To avoid ambiguity, {{math|Z/pZ}} or {{math|Z/(p)}} are often used to represent the integers modulo {{mvar|p}}.)
While it is possible to use the approach above to define {{mvar|p}}-adic numbers and explore their properties, just as in the case of real numbers other approaches are generally preferred. Hence we want to define a notion of infinite sum which makes these expressions meaningful, and this is most easily accomplished by the introduction of the {{mvar|p}}-adic metric. Two different but equivalent solutions to this problem are presented in the Constructions section below.
Notation
There are several different conventions for writing {{mvar|p}}-adic expansions. So far this article has used a notation for {{mvar|p}}-adic expansions in which powers of {{mvar|p}} increase from right to left. With this right-to-left notation the 3-adic expansion of {{frac|1|5}}, for example, is written as
When performing arithmetic in this notation, digits are carried to the left. It is also possible to write {{mvar|p}}-adic expansions so that the powers of {{mvar|p}} increase from left to right, and digits are carried to the right. With this left-to-right notation the 3-adic expansion of {{frac|1|5}} is
{{mvar|p}}-adic expansions may be written with other sets of digits instead of {0, 1, …, {{math|p − 1}}}. For example, the 3-adic expansion of 1/5 can be written using balanced ternary digits {1,0,1} as
In fact any set of {{mvar|p}} integers which are in distinct residue classes modulo {{mvar|p}} may be used as {{mvar|p}}-adic digits. In number theory, Teichmüller representatives are sometimes used as digits.[13]
Constructions
Analytic approach
{{see also|p-adic order}}| {{mvar|p}} = 2 | ← distance = 1 → | ||||||||
| ← d = ½ → | ← d = ½ → | ||||||||
| ‹ d=¼ › | ‹ d=¼ › | ‹ d=¼ › | ‹ d=¼ › | ||||||
| ‹⅛› | ‹⅛› | ‹⅛› | ‹⅛› | ‹⅛› | ‹⅛› | ‹⅛› | ‹⅛› | ||
| ................................................ | |||||||||
| 17 | 10001 | J | |||||||
| 16 | 10000 | J | |||||||
| 15 | 1111 | L | |||||||
| 14 | 1110 | L | |||||||
| 13 | 1101 | L | |||||||
| 12 | 1100 | L | |||||||
| 11 | 1011 | L | |||||||
| 10 | 1010 | L | |||||||
| 9 | 1001 | L | |||||||
| 8 | 1000 | L | |||||||
| 7 | 111 | L | |||||||
| 6 | 110 | L | |||||||
| 5 | 101 | L | |||||||
| 4 | 100 | L | |||||||
| 3 | 11 | L | |||||||
| 2 | 10 | L | |||||||
| 1 | 1 | L | |||||||
| 0 | 0…000 | L | |||||||
| −1 | 1…111 | J | |||||||
| −2 | 1…110 | J | |||||||
| −3 | 1…101 | J | |||||||
| −4 | 1…100 | J | |||||||
| ················································ | |||||||||
| | 2-adic ({{math|1= {{mvar|p}} = 2 }}) arrangement of integers, from left to right. This shows a hierarchical subdivision pattern common for ultrametric spaces. Points within a distance 1/8 are grouped in one colored strip. A pair of strips within a distance 1/4 has the same chroma, four strips within a distance 1/2 have the same hue. The hue is determined by the least significant bit, the saturation – by the next (21) bit, and the brightness depends on the value of 22 bit. Bits (digit places) which are less significant for the usual metric are more significant for the {{mvar|p}}-adic distance. | ||||||||
The real numbers can be defined as equivalence classes of Cauchy sequences of rational numbers; this allows us to, for example, write 1 as 1.000… = 0.999… . The definition of a Cauchy sequence relies on the metric chosen, though, so if we choose a different one, we can construct numbers other than the real numbers. The usual metric which yields the real numbers is called the Euclidean metric.
For a given prime {{mvar|p}}, we define the p-adic absolute value in {{math|Q}} as follows:
for any non-zero rational number {{mvar|x}}, there is a unique integer {{mvar|n}} allowing us to write {{math|1=x = pn(a/b)}}, where neither of the integers a and b is divisible by {{mvar|p}}. Unless the numerator or denominator of {{mvar|x}} in lowest terms contains {{mvar|p}} as a factor, {{mvar|n}} will be 0. Now define {{math|1=|x|p = p−n}}. We also define {{math|1=|0|p = 0}}.
For example with {{math|1=x = 63/550 = 2−1·32·5−2·7·11−1}}
This definition of {{math||x|p}} has the effect that high powers of {{mvar|p}} become "small".
By the fundamental theorem of arithmetic, for a given non-zero rational number x there is a unique finite set of distinct primes  and a corresponding sequence of non-zero integers
and a corresponding sequence of non-zero integers  such that:
such that:
It then follows that  for all
for all  , and
, and 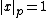 for any other prime
for any other prime 
The {{mvar|p}}-adic absolute value defines a metric dp on {{math|Q}} by setting
The field {{math|Qp}} of {{mvar|p}}-adic numbers can then be defined as the completion of the metric space ({{math|Q}}, dp); its elements are equivalence classes of Cauchy sequences, where two sequences are called equivalent if their difference converges to zero. In this way, we obtain a complete metric space which is also a field and contains {{math|Q}}.
It can be shown that in {{math|Qp}}, every element x may be written in a unique way as
where k is some integer such that ak ≠ 0 and each ai is in {0, …, {{math|p − 1}} }. This series converges to x with respect to the metric dp.
With this absolute value, the field {{math|Qp}} is a local field.
Ostrowski's theorem states that each absolute value on {{math|Q}} is equivalent either to the Euclidean absolute value, the trivial absolute value, or to one of the {{mvar|p}}-adic absolute values for some prime {{mvar|p}}. Each absolute value (or metric) leads to a different completion of {{math|Q}}. (With the trivial absolute value, {{math|Q}} is already complete.)
Algebraic approach
In the algebraic approach, we first define the ring of {{mvar|p}}-adic integers, and then construct the field of fractions of this ring to get the field of {{mvar|p}}-adic numbers.
We start with the inverse limit of the rings
{{math|Z/pnZ}} (see modular arithmetic): a {{mvar|p}}-adic integer m is then a sequence(an)n≥1 such that an is in
{{math|Z/pnZ}}, and if n ≤ m, thenan ≡ am (mod pn).
Every natural number m defines such a sequence (an) by an = m mod pn and can therefore be regarded as a {{mvar|p}}-adic integer. For example, in this case 35 as a 2-adic integer would be written as the sequence (1, 3, 3, 3, 3, 35, 35, 35, …).
The operators of the ring amount to pointwise addition and multiplication of such sequences. This is well defined because addition and multiplication commute with the "mod" operator; see modular arithmetic.
Moreover, every sequence (an) where the first element is not 0 has an inverse. In that case, for every n, an and p are coprime, and so an and pn are relatively prime. Therefore, each an has an inverse mod pn, and the sequence of these inverses, (bn), is the sought inverse of (an). For example, consider the {{mvar|p}}-adic integer corresponding to the natural number 7; as a 2-adic number, it would be written (1, 3, 7, 7, 7, 7, 7, ...). This object's inverse would be written as an ever-increasing sequence that begins (1, 3, 7, 7, 23, 55, 55, 183, 439, 439, 1463 ...). Naturally, this 2-adic integer has no corresponding natural number.
Every such sequence can alternatively be written as a series. For instance, in the 3-adics, the sequence (2, 8, 8, 35, 35, ...) can be written as {{math|2 + 2·3 + 0·32 + 1·33 + 0·34 + ...}} The partial sums of this latter series are the elements of the given sequence.
The ring of {{mvar|p}}-adic integers has no zero divisors, so we can take the field of fractions to get the field {{math|Qp}} of {{mvar|p}}-adic numbers. Note that in this field of fractions, every non-integer {{mvar|p}}-adic number can be uniquely written as {{math|p−n u}} with a natural number n and a unit {{math|u}} in the {{mvar|p}}-adic integers. This means that
Note that {{math|S−1 A}}However,  .
.
9. ^{{Harv|Kelley|2008|pp=22–25}}
10. ^{{cite web|last=Bogomolny|first=Alexander|authorlink= Alexander Bogomolny |title=p-adic Expansions|url=http://www.cut-the-knot.org/blue/p-adicExpansion.shtml}}
11. ^{{cite web|last=Koç|first=Çetin|title=A Tutorial on p-adic Arithmetic|url=https://koclab.cs.ucsb.edu/docs/koc/r09.pdf|format=PDF}}
12. ^{{cite web|last=Madore|first=David|title=A first introduction to p-adic numbers|url=http://www.madore.org/~david/math/padics.pdf|format=PDF}}
13. ^{{Harv|Hazewinkel|2009|p=342}}
14. ^{{Harv|Robert|2000|loc=Chapter 1 Section 1.1}}
15. ^{{Harv|Robert|2000|loc=Chapter 1 Section 2.3}}
16. ^{{Harv|Gouvêa|1997|loc=Corollary 3.3.8}}
17. ^{{Harv|Gouvêa|1997|loc=Corollary 5.3.10}}
18. ^{{Harv|Gouvêa|1997|loc=Theorem 5.7.4}}
19. ^1 2 {{Harv|Cassels|1986|p=149}}
20. ^1 {{Harv|Koblitz|1980|p=13}}
21. ^{{Harv|Gouvêa|1997|loc=Proposition 5.7.8}}
22. ^{{Harv|Gouvêa|1997|loc=Proposition 3.4.2}}
23. ^{{Harv|Robert|2000|loc=Section 4.1}}
24. ^{{Harv|Robert|2000|loc=Section 5.1}}
25. ^{{Harv|Hehner|Horspool|1979|pp=124–134}}
Citations
{{Reflist}}References
{{refbegin}}- {{Citation |last=Cassels |first=J. W. S. |authorlink=J. W. S. Cassels |title=Local Fields |series=London Mathematical Society Student Texts |volume=3 |publisher=Cambridge University Press |year=1986 |isbn=0-521-31525-5 |zbl=0595.12006}}
- {{citation|title=Theory of Algebraic Functions of One Variable|volume=39|series=History of mathematics|first1=Richard|last1=Dedekind|author1-link=Richard Dedekind|first2=Heinrich|last2=Weber|author2-link=Heinrich Martin Weber|publisher=American Mathematical Society|year=2012|isbn=978-0-8218-8330-3}}. — Translation into English by John Stillwell of Theorie der algebraischen Functionen einer Veränderlichen (1882).
- {{Citation|last=Gouvêa|first=F. Q.|author-link=F. Q. Gouvêa|date=March 1994|title=A Marvelous Proof|journal=American Mathematical Monthly|pages=203–222|volume=101|issue=3 |jstor=2975598|doi=10.2307/2975598}}
- {{Citation |last=Gouvêa |first=Fernando Q. |year=1997 |title=p-adic Numbers: An Introduction |edition=2nd |publisher=Springer |isbn=3-540-62911-4 | zbl=0874.11002}}
- {{citation|title=Handbook of Algebra|volume=6|editor-first=M.|editor-last=Hazewinkel|publisher=North Holland|date=2009|isbn=978-0-444-53257-2|page=342|url={{Google books|yimXZ-7L9ZoC|page=342|plainurl=yes}}}}
- {{Citation|last=Hehner|first=Eric C. R.|author-link=Eric C. R. Hehner|last2=Horspool|first2=R. Nigel|author2-link=R. Nigel Horspool|year=1979|title=A new representation of the rational numbers for fast easy arithmetic|journal=SIAM Journal on Computing|pages=124–134 |volume=8 |issue=2 |doi=10.1137/0208011 |url=https://www.researchgate.net/profile/Eric_Hehner/publication/220617770_A_New_Representation_of_the_Rational_Numbers_for_Fast_Easy_Arithmetic/links/0912f5058d7a114e7f000000.pdf}}
- {{Citation | last = Hensel | first = Kurt | author-link=Kurt Hensel | title = Über eine neue Begründung der Theorie der algebraischen Zahlen | journal = Jahresbericht der Deutschen Mathematiker-Vereinigung | volume = 6 | year = 1897 | issue = 3 | pages = 83–88 | url = http://www.digizeitschriften.de/resolveppn/GDZPPN00211612X&L=2}}
- {{Citation|last1=Kelley|first1=John L.|author-link=John Leroy Kelley|title=General Topology|date=2008|origyear=1955|publisher=Ishi Press|location=New York|isbn=978-0-923891-55-8}}
- {{Citation |last=Koblitz |first=Neal |authorlink=Neal Koblitz |title=p-adic analysis: a short course on recent work |series=London Mathematical Society Lecture Note Series |volume=46 |publisher=Cambridge University Press |year=1980 |isbn=0-521-28060-5 |zbl=0439.12011}}
- {{Citation |last=Robert |first=Alain M. |year=2000 |title=A Course in p-adic Analysis |publisher=Springer |isbn=0-387-98669-3}}
Further reading
{{refbegin}}- {{Citation |last=Bachman |first=George |title=Introduction to p-adic Numbers and Valuation Theory |year=1964 |publisher=Academic Press |isbn=0-12-070268-1}}
- {{Citation|last=Borevich|first=Z. I.|author-link=Zenon Ivanovich Borevich|last2=Shafarevich|first2=I. R.|author2-link=Igor Rostislavovich Shafarevich|year=1986|title=Number Theory|publisher=Academic Press|location=Boston, MA|series=Pure and Applied Mathematics|volume=20|isbn=978-0-12-117851-2|url={{Google books|njgVUjjO-EAC|Number Theory|plainurl=yes}}|mr=0195803}}
- {{Citation |last=Koblitz |first=Neal |authorlink=Neal Koblitz |year=1984 | series=Graduate Texts in Mathematics | volume=58 | title=p-adic Numbers, p-adic Analysis, and Zeta-Functions | edition=2nd |publisher=Springer |isbn=0-387-96017-1}}
- {{Citation | last=Mahler | first=Kurt | authorlink=Kurt Mahler | title=p-adic numbers and their functions | edition=2nd | zbl=0444.12013 | series=Cambridge Tracts in Mathematics | volume=76 | location=Cambridge |publisher=Cambridge University Press | year=1981 | isbn=0-521-23102-7 }}
- {{Citation |last=Steen |first=Lynn Arthur |authorlink=Lynn Arthur Steen |year=1978 |title=Counterexamples in Topology |publisher=Dover |isbn=0-486-68735-X}}
External links
{{Commonscat|P-adic numbers}}- {{MathWorld|urlname=p-adicNumber|title=p-adic Number}}
- {{planetmath reference|id=3118|title=p-adic integers}}
- p-adic number at Springer On-line Encyclopaedia of Mathematics
- Completion of Algebraic Closure – on-line lecture notes by Brian Conrad
- An Introduction to p-adic Numbers and p-adic Analysis - on-line lecture notes by Andrew Baker, 2007
- Efficient p-adic arithmetic (slides)
- Introduction to p-adic numbers
- Garkan-e Shomali
- Garkan-e Shomali Rural District
- Garkan-e Sofla
- Garkan Jonubi
- Garkan Jonubi District
- Garkan Rural District
- Garkarud
- Gar Kaz
- Garkaz
- Garkaz-e Tazeh Yal
- Garkaz Mahalleh
- Garker
- Garkesh
- Garkhashab
- Garkhashab-e Abdi
- Garkhashab-e Sofla
- Garkha (Vidhan Sabha constituency)
- Garkhonkan
- Garki Project
- Garkiyeh
- Garklein recorder
- Gar Kodu
- Gar Kola
- Garkolagh
- Garkolagh Neshin