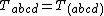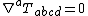“Bel–Robinson tensor”的意思、由来-开放百科全书

词条

Bel–Robinson tensor

释义

References

In general relativity and differential geometry, the Bel–Robinson tensor is a tensor defined in the abstract index notation by:

Alternatively,

where 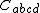is the Weyl tensor. It was introduced by Lluís Bel in 1959.^[1]^[2] The Bel–Robinson tensor is constructed from the Weyl tensor in a manner analogous to the way the electromagnetic stress–energy tensor is built from the electromagnetic tensor. Like the electromagnetic stress–energy tensor, the Bel–Robinson tensor is totally symmetric and traceless:

In general relativity, there is no unique definition of the local energy of the gravitational field. The Bel–Robinson tensor is a possible definition for local energy, since it can be shown that whenever the Ricci tensor vanishes (i.e. in vacuum), the Bel–Robinson tensor is divergence-free:

References

1. ^{{citation|first1=L.|last1=Bel|title=Introduction d'un tenseur du quatrième ordre|journal=Comptes rendus hebdomadaires des séances de l'Académie des sciences|volume=248|page=1297|year=1959|url=http://gallica.bnf.fr/ark:/12148/bpt6k32002/f1321.image.langEN}}
2. ^{{citation|first1=J. M. M.|last1=Senovilla|title=Editor's Note: Radiation States and the Problem of Energy in General Relativity by Louis Bel|journal=General Relativity and Gravitation|volume=32|page=2043|year=2000|doi=10.1023/A:1001906821162|bibcode=2000GReGr..32.2043S}}

2 : Tensors in general relativity|Differential geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。