- Motivation
- Definition
- Simpson's alternative definition
- Major theorems
- See also
- References
In order theory a better-quasi-ordering or bqo is a quasi-ordering that does not admit a certain type of bad array. Every better-quasi-ordering is a well-quasi-ordering.
Motivation
Though well-quasi-ordering is an appealing notion, many important infinitary operations do not preserve well-quasi-orderedness.
An example due to Richard Rado illustrates this.[1]
In a 1965 paper Crispin Nash-Williams formulated the stronger notion of better-quasi-ordering in order to prove that the class of trees of height ω is well-quasi-ordered under the topological minor relation.[2] Since then, many quasi-orderings have been proven to be well-quasi-orderings by proving them to be better-quasi-orderings. For instance, Richard Laver established Fraïssé's conjecture by proving that the class of scattered linear order types is better-quasi-ordered. More recently, Carlos Martinez-Ranero has proven that, under the Proper Forcing Axiom, the class of Aronszajn lines is better-quasi-ordered under the embeddability relation.[4]
Definition
It is common in better-quasi-ordering theory to write 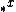 for the sequence
for the sequence  with the first term omitted. Write
with the first term omitted. Write 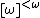 for the set of finite, strictly increasing sequences with terms in
for the set of finite, strictly increasing sequences with terms in 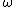 , and define a relation
, and define a relation  on
on 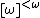 as follows:
as follows: 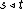 if there is
if there is 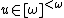 such that
such that  is a strict initial segment of
is a strict initial segment of  and
and 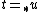 . The relation
. The relation  is not transitive.
is not transitive.
A block  is an infinite subset of
is an infinite subset of 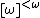 that contains an initial segment{{clarify|reason=Explain the notion of an "initial segment of a set" before use.|date=August 2018}} of every
that contains an initial segment{{clarify|reason=Explain the notion of an "initial segment of a set" before use.|date=August 2018}} of every
infinite subset of  . For a quasi-order
. For a quasi-order  , a
, a  -pattern is a function from some block
-pattern is a function from some block  into
into  . A
. A  -pattern
-pattern 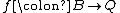 is said to be bad if
is said to be bad if 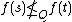 {{clarify|reason=Explain "≤Q" before use.|date=August 2018}} for every pair
{{clarify|reason=Explain "≤Q" before use.|date=August 2018}} for every pair 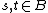 such that
such that 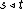 ; otherwise
; otherwise  is good. A quasi-ordering
is good. A quasi-ordering  is called a better-quasi-ordering if there is no bad
is called a better-quasi-ordering if there is no bad  -pattern.
-pattern.
In order to make this definition easier to work with, Nash-Williams defines a barrier to be a block whose elements are pairwise incomparable under the inclusion relation  . A
. A  -array is a
-array is a  -pattern whose domain is a barrier. By observing that every block contains a barrier, one sees that
-pattern whose domain is a barrier. By observing that every block contains a barrier, one sees that  is a better-quasi-ordering if and only if there is no bad
is a better-quasi-ordering if and only if there is no bad  -array.
-array.
Simpson's alternative definition
Simpson introduced an alternative definition of better-quasi-ordering in terms of Borel functions  , where
, where 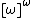 , the set of infinite subsets of
, the set of infinite subsets of 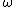 , is given the usual product topology.[5]
, is given the usual product topology.[5]
Let  be a quasi-ordering and endow
be a quasi-ordering and endow  with the discrete topology. A
with the discrete topology. A  -array is a Borel function
-array is a Borel function 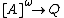 for some infinite subset
for some infinite subset  of
of 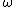 . A
. A  -array
-array  is bad if
is bad if 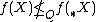 for every
for every 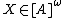 ;
;
 is good otherwise. The quasi-ordering
is good otherwise. The quasi-ordering  is a better-quasi-ordering if there is no bad
is a better-quasi-ordering if there is no bad  -array in this sense.
-array in this sense.
Major theorems
Many major results in better-quasi-ordering theory are consequences of the Minimal Bad Array Lemma, which appears in Simpson's paper[5] as follows. See also Laver's paper,[7] where the Minimal Bad Array Lemma was first stated as a result. The technique was present in Nash-Williams' original 1965 paper.
Suppose  is a quasi-order.{{clarify|reason=Should probably be "quasi-ordered set"?|date=August 2018}} A partial ranking
is a quasi-order.{{clarify|reason=Should probably be "quasi-ordered set"?|date=August 2018}} A partial ranking 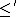 of
of  is a well-founded partial ordering of
is a well-founded partial ordering of  such that
such that 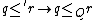 . For bad
. For bad  -arrays (in the sense of Simpson)
-arrays (in the sense of Simpson) 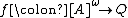 and
and 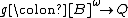 , define:
, define:
We say a bad  -array
-array  is minimal bad (with respect to the partial ranking
is minimal bad (with respect to the partial ranking 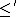 ) if there is no bad
) if there is no bad  -array
-array  such that
such that 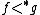 .
.
Note that the definitions of 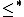 and
and  depend on a partial ranking
depend on a partial ranking 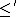 of
of  . Note also that the relation
. Note also that the relation  is not the strict part of the relation
is not the strict part of the relation 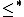 .
.
Theorem (Minimal Bad Array Lemma). Let  be a quasi-order equipped with a partial ranking and suppose
be a quasi-order equipped with a partial ranking and suppose  is a bad
is a bad  -array. Then there is a minimal bad
-array. Then there is a minimal bad  -array
-array  such that
such that 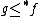 .
.
See also
- Well-quasi-ordering
- Well-order
References
2. ^1 {{cite journal | last1 = Nash-Williams | first1 = C. St. J. A. | authorlink1 = Crispin Nash-Williams | title = On well-quasi-ordering infinite trees | journal = Mathematical Proceedings of the Cambridge Philosophical Society | volume = 61 | issue = 3 | year = 1965 | pages = 697–720 | issn = 0305-0041 | doi = 10.1017/S0305004100039062 | mr = 0175814 | bibcode = 1965PCPS...61..697N}}
3. ^1 {{cite journal | last = Rado | first = Richard | authorlink = Richard Rado | title = Partial well-ordering of sets of vectors | journal = Mathematika | year = 1954 | volume = 1 | pages = 89–95 | doi = 10.1112/S0025579300000565 | mr = 0066441 | issue = 2}}
4. ^1 2 {{cite book | last = Simpson | first = Stephen G. | chapter = BQO Theory and Fraïssé's Conjecture | title = Recursive Aspects of Descriptive Set Theory | editor1-last = Mansfield | editor1-first = Richard | editor2-last = Weitkamp | editor2-first = Galen | publisher = The Clarendon Press, Oxford University Press | year = 1985 | pages = 124–38 | mr = 786122 | isbn = 978-0-19-503602-2}}
5. ^1 {{cite book | last = Laver | first = Richard | chapter = Better-quasi-orderings and a class of trees | title = Studies in foundations and combinatorics | editor1-last = Rota | editor1-first = Gian-Carlo | publisher = Academic Press | year = 1978 | pages = 31–48 | mr = 0520553 | isbn = 978-0-12-599101-8}}
}}
- Embrujo antillano
- Embrunman
- Embryo (album)
- Embryobionta
- Embryocardia
- Embryo development of the first month
- Embryoglossa
- Embryoglossa aethiopicalis
- Embryoglossa bipuncta
- Embryoglossa submarginata
- Embryoglossa variegata
- Embryokine
- Embryologic development
- Embryology of digestive system and the body cavities
- Embryology of heart
- Embryology of the heart
- Embryonal fyn-associated substrate
- Embryonated
- Embryonic adnexa
- Embryonic age
- Embryonic Anomaly
- Embryonic cannibalism
- Embryonic cell cleavage
- Embryonic coelom
- Embryonic coeloms

