“Binary game”的意思、由来-开放百科全书

词条

Binary game

释义

References

In mathematics, the binary game is a topological game introduced by Stanislaw Ulam in 1935 in an addendum to problem 43 of the Scottish book as a variation of the Banach–Mazur game.

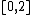In the binary game, one is given a fixed subset X of the set {0,1}^N of all sequences of 0s and 1s. The players take it in turn to choose a digit 0 or 1, and the first player wins if the sequence they form lies in the set X. Another way to represent this game is to pick a subset of the interval on the real line, then the players alternatively choose binary digits 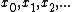. Player I wins the game if and only if the binary number 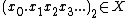, that is, 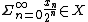. See,^[1] page 237.

The binary game is sometimes called Ulam's game, but "Ulam's game" usually refers to the Rényi–Ulam game.

References

1. ^{{cite journal|last1=Telgársky|first1=Rastislav|title=Topological Games: On the 50th Anniversary of the Banach-Mazur Game|journal=Rocky Mountain Journal of Mathematics|date=Spring 1987|volume=17|issue=2|pages=227–276|url=http://www.telgarsky.com/1987-RMJM-Telgarsky-Topological-Games.pdf}}

1 : Topological games

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。