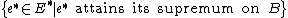- See also
- References
In mathematics, the Bishop–Phelps theorem is a theorem about the topological properties of Banach spaces named after Errett Bishop and Robert Phelps, who published its proof in 1961.
Its statement is as follows.
Let B ⊂ E be a bounded, closed, convex set of a real Banach space E. Then the set
is norm-dense in the dual. Note, this theorem fails for complex Banach spaces [1]
See also
- Banach–Alaoglu theorem
- Eberlein–Šmulian theorem
- Mazur's lemma
- James' theorem
- Goldstine theorem
References
1. ^{{cite journal|authorlink1=Victor Lomonosov|last1=Lomonosov|first1=Victor|title=A counterexample to the Bishop-Phelps theorem in complex spaces|journal=Israel J. Math.|date=2000|volume=115|pages=25–28}}
- {{cite journal|last1=Bishop|first1=Errett|authorlink1=Errett Bishop|last2=Phelps|first2=R. R.|authorlink2=Robert R. Phelps|title=A proof that every Banach space is subreflexive|journal=Bulletin of the American Mathematical Society|volume=67|year=1961|pages=97–98|mr=123174|ref=harv|doi=10.1090/s0002-9904-1961-10514-4}}
1 : Theorems in functional analysis
- Events in 1799
- Events in 18
- Events in 180
- Events in 1800
- Events in 1801
- Events in 1802
- Events in 1803
- Events in 1804
- Events in 1805
- Events in 1806
- Events in 1807
- Events in 1808
- Events in 1809
- Events in 181
- Events in 1810
- Events in 1811
- Events in 1812
- Events in 1813
- Events in 1814
- Events in 1815
- Events in 1816
- Events in 1817
- Events in 1818
- Events in 1819
- Events in 182