函数极限的性质hanshu jixian de xingzhi

❶ （唯一性） 若当x→x₀时，函数f (x)存在极限，则它只有一个极限。

❷（局部有界性） 若当x→x ₀时函数f (x)存在极限，则存在某个正数δ₀，使得当0<|x-x₀| <δ₀时，有|f (x) |≤M，其中M是正常数。

❸若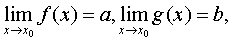且a0，使得当0<|x-x₀|<δ₀时，有f (x)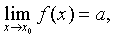推论1 （局部保号性） 若且a>0，则存在正数δ₀，使得当0<|x-x₀|<δ₀时，有f (x)>0。
推论2 若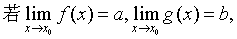且存在某个正数δ₀，使得当0<|x-x₀| <δ₀时，有f (x)≤g (x)，则a≤b。

❹若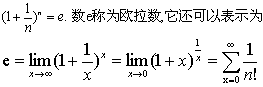且存在正数δ₀，使得当0< |x-x₀| <δ₀时，有f (x) ≤h (x) ≤g (x)，则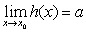

❺ 海涅定理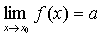的充分必要条件是，在函数f (x)的定义域内，对任何以x₀为极限的数列{x_n},x_n≠x₀，都有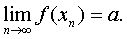
性质
❺即为海涅定理，此定理给出了函数极限与数列极限之间的关系.根据海涅定理，可利用数列极限的某些定理来推断函数极限的相应定理。利用海涅定理的必要性，判别某些函数不存在极限比较方便。
上面仅就极限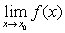给出了函数极限的基本性质，其他类型的极限如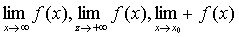等也有类似的性质。