函数的间断点hanshu de jianduandian

设函数f(x) 定义域为E。若x₀∈E或x₀为E的聚点，且等式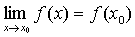在点x₀不成立，即f ( x)与x ₀满足如下三条之一：❶函数f (x)在点x₀没有定义；
❷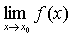不存在；
❸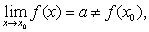则称点x₀为函数f (x) 的间断点或不连续点。
函数的间断点分为两类：
❶ 若函数f (x)在点x₀有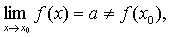则称点x₀为函数f (x) 的可去间断点。

❷ 若函数f(x)在点x₀存在左极限和右极限，但f (x₀-0) ≠f (x₀+0)，则称点x₀为函数f (x)的跳跃间断点。数|f (x₀-0) -f (x₀+0) |称为函数f(x) 在点x₀的跳跃度。
可去间断点与跳跃间断点统称为第一类间断点。

❸ 若在f (x₀-0)与f (x₀+0) 中至少有一个不存在，则称点x₀为函数f (x)的第二类间断点。若在f (x₀-0)与f (x₀+0)中至少有一个是无穷大量，则称点x0为无穷型间断点。