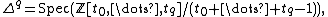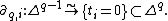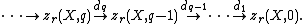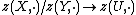“Bloch's higher Chow group”的意思、由来-开放百科全书

词条

Bloch's higher Chow group

释义

Definition
Localization theorem
References

In algebraic geometry, Bloch's higher Chow groups, a generalization of Chow group, is a precursor and a basic example of motivic cohomology (for smooth varieties). It was introduced by Spencer Bloch {{harv|Bloch|1986}} and the basic theory has been developed by Bloch and Marc Levine.

In more precise terms, a theorem of Voevodsky^[1] implies: for a smooth scheme X over a field and integers p, q, there is a natural isomorphism

between motivic cohomology groups and higher Chow groups.

Definition

Let X be an algebraic scheme over a field (“algebraic” means separated and of finite type).

For each integer 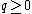, define

which is an algebraic analog of a standard q-simplex. For each sequence 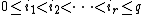, the closed subscheme 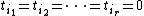, which is isomorphic to 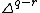, is called a face of .

For each i, there is the embedding

We write 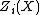for the group of algebraic i-cycles on X and 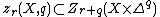for the subgroup generated by closed subvarieties that intersect properly with 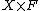for each face F of .

Since 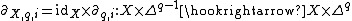is an effective Cartier divisor, there is the Gysin homomorphism:

,

that (by definition) maps a subvariety V to the intersection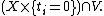

Define the boundary operator 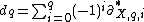which yields the chain complex

Finally, the q-th higher Chow group of X is defined as the q-th homology of the above complex:

(More simply, since is naturally a simplicial abelian group, in view of the Dold–Kan correspondence, higher Chow groups can also be defined as homotopy groups .)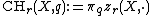

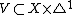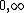For example, if ^[2] is a closed subvariety such that the intersections with the faces are proper, then

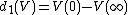and this means, by Proposition 1.6. in Fulton’s intersection theory, that the image of is precisely the group of cycles rationally equivalent to zero; that is,

the r-th Chow group of X.

Localization theorem

{{harv|Bloch|1994}} showed that, given an open subset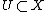

, for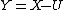

is a homotopy equivalence. In particular, if has pure codimension, then it yields the long exact sequence for higher Chow groups (called the localization sequence).

References

1. ^{{harvnb|Voevodsky|2002}}
2. ^Here, we identify

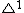with a subscheme of

and then, without loss of generality, assume one vertex is the origin 0 and the other is ∞.

S. Bloch, “Algebraic cycles and higher K-theory,” Adv. Math. 61 (1986), 267–304.
S. Bloch, “The moving lemma for higher Chow groups,” J. Algebraic Geom. 3, 537–568 (1994)
Peter Haine, An Overview of Motivic Cohomology
Vladmir Voevodsky, “Motivic cohomology groups are isomorphic to higher Chow groups in any characteristic,” International Mathematics Research Notices 7 (2002), 351–355.

1 : Algebraic geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。