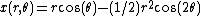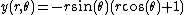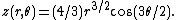“Bour's minimal surface”的意思、由来-开放百科全书

In mathematics, Bour's minimal surface is a two-dimensional minimal surface, embedded with self-crossings into three-dimensional Euclidean space. It is named after Edmond Bour, whose work on minimal surfaces won him the 1861 mathematics prize of the French Academy of Sciences.^[1]

Description

Bour's surface crosses itself on three coplanar rays, meeting at equal angles at the origin of the space. The rays partition the surface into six sheets, topologically equivalent to half-planes; three sheets lie in the halfspace above the plane of the rays, and three below. Four of the sheets are mutually tangent along each ray.

Equation

The points on the surface may be parameterized in polar coordinates by a pair of numbers (r,θ). Each such pair corresponds to a point in three dimensions according to the parametric equations^[2]

The surface can also be expressed as the solution to a polynomial equation of order 16 in the Cartesian coordinates of the three-dimensional space.

Properties

The Weierstrass–Enneper parameterization, a method for turning certain pairs of functions over the complex numbers into minimal surfaces, produces this surface for the two functions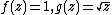

. It was proved by Bour that surfaces in this family are developable onto a surface of revolution.^[3]

References

1. ^{{MacTutor|id=Bour|title=Edmond Bour}}.
2. ^Weisstein, Eric W. "Bour's Minimal Surface." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/BoursMinimalSurface.html
3. ^Ulrich Dierkes, Stefan Hildebrandt, Friedrich Sauvigny, Minimal Surfaces, Volume 1. Springer 2010