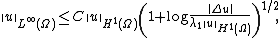- See also
- Notes
- References
In mathematical analysis, the Brezis–Gallouet inequality,[1] named after Haïm Brezis and Thierry Gallouet, is an inequality valid in 2 spatial dimensions. It shows that a function of two variables which is sufficiently smooth is (essentially) bounded, and provides an explicit bound, which depends only logarithmically on the second derivatives. It is useful in the study of partial differential equations.
Let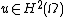 
where 
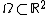. Then the Brézis–Gallouet inequality states that there exists a constant 
such that
where 
is the Laplacian, and 
is its first eigenvalue.
See also
- Ladyzhenskaya inequality
- Agmon's inequality
Notes
1. ^Nonlinear Schrödinger evolution equation, Nonlinear Analysis TMA 4, 677. (1980)
References
- {{cite book | last1 = Foias | first1 = Ciprian | authorlink=Ciprian Foias |last2=Manley|first2=O.|last3=Rosa|first3=R.|last4=Temam|first4=R.| title = Navier–Stokes Equations and Turbulence | publisher = Cambridge University Press | location = Cambridge | year = 2001 | isbn = 0-521-36032-3 }}
2 : Theorems in analysis|Inequalities
- Al-hikma al-sharifa
- Al Hikmah University
- Al-Hilal (Al-Fasher)
- Al-Hilal (basketball)
- Alhilal Benghazi S.C.
- Al Hilal (district)
- Al-Hilal English School, Manki
- Al Hilal English School, Manki
- Al-Hilal ESC (Al-Fasher)
- Al-Hilal FC (Juba)
- Al Hilal (film)
- Al-Hilal (journal)
- Al Hilal Juba
- Al-Hilal (Juba) FC
- Al-Hilal Kadougli
- Al-Hilal (Kadougli)
- Al-Hilal Kaduqli
- Al-Hilal (magazine)
- Al-Hilal Omdurman
- Al-Hilal (Port Sudan)
- Al Hilal Riyadh
- Al-Hilal (Salalah)
- Al-Hilal SC Kadougli
- Al-Hilal SC (Port Sudan)
- AlHilal Stadium