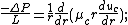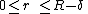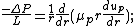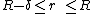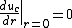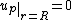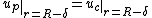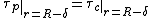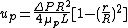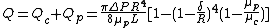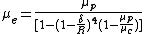- Mathematical modeling Governing equations Boundary conditions Velocity profiles Volumetric flow rate for cell-free and core regions
- See also
- References
In small capillary hemodynamics, the cell-free layer is a near-wall layer of plasma absent of red blood cells since they are subject to migration to the capillary center in Poiseuille flow.[1] Cell-free marginal layer model is a mathematical model which tries to explain Fåhræus–Lindqvist effect mathematically.
Mathematical modeling
Governing equations
Consider steady flow of blood through a capillary of radius  . The capillary cross section can be divided into a core region and cell-free plasma region near the wall. The governing equations for both regions can be given by the following equations:[2]
. The capillary cross section can be divided into a core region and cell-free plasma region near the wall. The governing equations for both regions can be given by the following equations:[2]
where:
is the pressure drop across the capillary
is the length of capillary
is velocity in core region
is velocity of plasma in cell-free region
is viscosity in core region
is viscosity of plasma in cell-free region
is the cell-free plasma layer thickness
Boundary conditions
The boundary conditions to obtain the solution for the two differential equations presented above are that the velocity gradient is zero in the tube center, no slip occurs at the tube wall and the velocity and the shear stress are continuous at the interface between the two zones. These boundary conditions can be expressed mathematically as:
Velocity profiles
Integrating governing equations with respect to r and applying the above discussed boundary conditions will result in:
Volumetric flow rate for cell-free and core regions
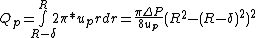
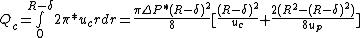
Total volumetric flow rate is the algebraic sum of the flow rates in core and plasma region. The expression for the total volumetric flow rate can be written as:
Comparison with the viscosity which applies in the Poiseuille flow yields effective viscosity, 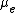 as:
as:
It can be realized when the radius of the blood vessel is much larger than the thickness of the cell-free plasma layer, the effective viscosity is equal to bulk blood viscosity 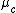 at high shear rates (Newtonian fluid).
at high shear rates (Newtonian fluid).
Conservation of Mass Requires:
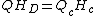
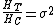
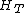 = Average Red Blood Cell (RBC) volume fraction in small capillary
= Average Red Blood Cell (RBC) volume fraction in small capillary
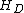 = Average RBC volume fraction in the core layer
= Average RBC volume fraction in the core layer
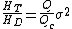 ,
, 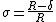

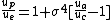
Blood viscosity as a fraction of hematocrit:
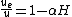
See also
- Fåhræus–Lindqvist effect
- Blood viscosity
- hemodynamics
References
2. ^{{cite book|last=Krishnan B. Chandran|first=Alit P. Yoganathan , Ajit P. Yoganathan , Stanley E. Rittgers|title=Biofluid mechanics : the human circulation|year=2007|publisher=CRC/Taylor & Francis|location=Boca Raton|isbn=978-0-8493-7328-2|url=https://www.amazon.com/Biofluid-Mechanics-Circulation-Krishnan-Chandran/dp/084937328X}}
- Qalicheh Bolagh
- Qalidin
- Qalij Khani
- Qalilu
- Qalini
- Qalin Qayeh
- Qalipu Miꞌkmaq First Nation Band
- Qaliqala
- Qalizan
- Qaljehi
- Qaljeh'i
- Qalkhanchak
- Qalkhani
- Qalkhani Rural District
- Qallah-i-Maidan
- Qalla Pola
- Qalla Qhata
- Qallat
- Qallat-e Pa'in
- Qallat-e Pain
- Qalleh Jam
- Qalleh Vari
- Qallin
- Qallwa
- Qallwa (Andagua)