“Chiral homology”的意思、由来-开放百科全书

词条

Chiral homology

释义

See also
References

In mathematics, chiral homology, introduced by Alexander Beilinson and Vladimir Drinfeld, is, in their words, "a “quantum” version of (the algebra of functions on) the space of global horizontal sections of an affine 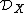-scheme (i.e., the space of global solutions of a system of non-linear differential equations)."

Jacob Lurie's topological chiral homology gives an analog for manifolds.^[1]

References

1. ^{{nlab|id=On+the+Classification+of+Topological+Field+Theories|title=outline of "On the Classification of Topological Field Theories"}}

{{cite book|last1=Beilinson|first1=Alexander|authorlink1=Alexander Beilinson|last2=Drinfeld|first2=Vladimir|authorlink2=Vladimir Drinfeld | title=Chiral algebras|date=2004|publisher=American Mathematical Society|isbn=0-8218-3528-9|chapter=Chapter 4|url=http://www.math.uchicago.edu/~mitya/langlands.html}}

1 : Homological algebra

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

See also

References