- See also
- References
A conjecture of Paul Erdős and Norman Oler states that, if {{mvar|n}} is a triangular number, then the optimal packings of {{math|n − 1}} and of {{mvar|n}} circles have the same side length: that is, according to the conjecture, an optimal packing for {{math|n − 1}} circles can be found by removing any single circle from the optimal hexagonal packing of {{mvar|n}} circles.[4] This conjecture is now known to be true for {{math|n ≤ 15}}.[5]
Minimum solutions for the side length of the triangle:[1]
| Number of circles | Is triangular | Length | Area |
|---|---|---|---|
| 1 | True |  = 3.464... = 3.464... | 5.196... |
| 2 | False |  = 5.464... = 5.464... | 12.928... |
| 3 | True |  = 5.464... = 5.464... | 12.928... |
| 4 | False |  = 6.928... = 6.928... | 20.784... |
| 5 | False | 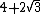 = 7.464... = 7.464... | 24.124... |
| 6 | True | 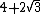 = 7.464... = 7.464... | 24.124... |
| 7 | False |  = 8.928... = 8.928... | 34.516... |
| 8 | False | 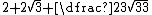 = 9.293... = 9.293... | 37.401... |
| 9 | False | 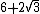 = 9.464... = 9.464... | 38.784... |
| 10 | True | 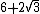 = 9.464... = 9.464... | 38.784... |
| 11 | False |  = 10.730... = 10.730... | 49.854... |
| 12 | False | 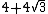 = 10.928... = 10.928... | 51.712... |
| 13 | False |  = 11.406... = 11.406... | 56.338... |
| 14 | False | 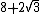 = 11.464... = 11.464... | 56.908... |
| 15 | True | 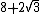 = 11.464... = 11.464... | 56.908... |
A closely related problem is to cover the equilateral triangle with a fixed number of equal circles, having as small a radius as possible.[6]
See also
- Circle packing in an isosceles right triangle
- Malfatti circles, a construction giving the optimal solution for three circles in an equilateral triangle
References
1. ^1 {{citation | last = Melissen | first = Hans | doi = 10.2307/2324212 | mr = 1252928 | issue = 10 | journal = The American Mathematical Monthly | pages = 916–925 | title = Densest packings of congruent circles in an equilateral triangle | volume = 100 | year = 1993}}.
2. ^{{citation | last1 = Melissen | first1 = J. B. M. | last2 = Schuur | first2 = P. C. | doi = 10.1016/0012-365X(95)90139-C | mr = 1356610 | issue = 1-3 | journal = Discrete Mathematics | pages = 333–342 | title = Packing 16, 17 or 18 circles in an equilateral triangle | volume = 145 | year = 1995}}.
3. ^{{citation | last1 = Graham | first1 = R. L. | author1-link = Ronald Graham | last2 = Lubachevsky | first2 = B. D. | mr = 1309122 | journal = Electronic Journal of Combinatorics | page = Article 1, approx. 39 pp. (electronic) | title = Dense packings of equal disks in an equilateral triangle: from 22 to 34 and beyond | url = http://www.combinatorics.org/Volume_2/Abstracts/v2i1a1.html | volume = 2 | year = 1995}}.
4. ^{{citation | last = Oler | first = Norman | doi = 10.4153/CMB-1961-018-7 | mr = 0133065 | journal = Canadian Mathematical Bulletin | pages = 153–155 | title = A finite packing problem | volume = 4 | year = 1961}}.
5. ^{{citation | last = Payan | first = Charles | doi = 10.1016/S0012-365X(96)00201-4 | mr = 1439300 | journal = Discrete Mathematics | language = French | pages = 555–565 | title = Empilement de cercles égaux dans un triangle équilatéral. À propos d'une conjecture d'Erdős-Oler | volume = 165/166 | year = 1997}}.
6. ^{{citation | last = Nurmela | first = Kari J. | mr = 1780209 | issue = 2 | journal = Experimental Mathematics | pages = 241–250 | title = Conjecturally optimal coverings of an equilateral triangle with up to 36 equal circles | url = http://projecteuclid.org/getRecord?id=euclid.em/1045952348 | volume = 9 | year = 2000 | doi=10.1080/10586458.2000.10504649}}.
{{Packing problem}}{{elementary-geometry-stub}}2. ^{{citation | last1 = Melissen | first1 = J. B. M. | last2 = Schuur | first2 = P. C. | doi = 10.1016/0012-365X(95)90139-C | mr = 1356610 | issue = 1-3 | journal = Discrete Mathematics | pages = 333–342 | title = Packing 16, 17 or 18 circles in an equilateral triangle | volume = 145 | year = 1995}}.
3. ^{{citation | last1 = Graham | first1 = R. L. | author1-link = Ronald Graham | last2 = Lubachevsky | first2 = B. D. | mr = 1309122 | journal = Electronic Journal of Combinatorics | page = Article 1, approx. 39 pp. (electronic) | title = Dense packings of equal disks in an equilateral triangle: from 22 to 34 and beyond | url = http://www.combinatorics.org/Volume_2/Abstracts/v2i1a1.html | volume = 2 | year = 1995}}.
4. ^{{citation | last = Oler | first = Norman | doi = 10.4153/CMB-1961-018-7 | mr = 0133065 | journal = Canadian Mathematical Bulletin | pages = 153–155 | title = A finite packing problem | volume = 4 | year = 1961}}.
5. ^{{citation | last = Payan | first = Charles | doi = 10.1016/S0012-365X(96)00201-4 | mr = 1439300 | journal = Discrete Mathematics | language = French | pages = 555–565 | title = Empilement de cercles égaux dans un triangle équilatéral. À propos d'une conjecture d'Erdős-Oler | volume = 165/166 | year = 1997}}.
6. ^{{citation | last = Nurmela | first = Kari J. | mr = 1780209 | issue = 2 | journal = Experimental Mathematics | pages = 241–250 | title = Conjecturally optimal coverings of an equilateral triangle with up to 36 equal circles | url = http://projecteuclid.org/getRecord?id=euclid.em/1045952348 | volume = 9 | year = 2000 | doi=10.1080/10586458.2000.10504649}}.
1 : Circle packing
- The Click List: Top 10 Videos
- The Click Song
- The Clicquot Club Eskimos
- The Client (1994 film)
- The Client (The Office)
- The Cliff
- The Cliff (Dynasty)
- The Cliffhanger
- The Cliffhanger: Edward Randy
- The Cliffhanger (The O.C. episode)
- The Clifford Ball
- The Cliffs
- The Cliffs of Insanity
- The Cliff Training Ground
- The Cliff (training ground)
- The Clift Royal Sonesta Hotel
- The Cliks
- The climate registry
- The Climate Registry
- The Climax
- The Climb (1999 film)
- The Climb (book)
- Theclinae
- The Clincher
- Theclini