- References
Circle packing in a right isosceles triangle is a packing problem where the objective is to pack n unit circles into the smallest possible isosceles right triangle.
Minimum solutions (lengths shown are length of leg) are shown in the table below.[1] Solutions to the equivalent problem of maximizing the minimum distance between n points in an isosceles right triangle, are known to be optimal for n< 8.[2] In 2011 a heuristic algorithm found 18 improvements on previously known optima, the smallest of which was for n=13.[3]
| Number of circles | Length |
|---|---|
| 1 | 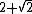 = 3.414... = 3.414... |
| 2 | 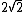 = 4.828... = 4.828... |
| 3 |  = 5.414... = 5.414... |
| 4 |  = 6.242... = 6.242... |
| 5 |  = 7.146... = 7.146... |
| 6 |  = 7.414... = 7.414... |
| 7 | 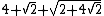 = 8.181... = 8.181... |
| 8 | 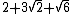 = 8.692... = 8.692... |
| 9 |  = 9.071... = 9.071... |
| 10 |  = 9.414... = 9.414... |
| 11 |  = 10.059... = 10.059... |
| 12 | 10.422... |
| 13 | 10.798... |
| 14 |  = 11.141... = 11.141... |
| 15 | 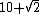 = 11.414... = 11.414... |
References
1. ^{{cite web|url=http://hydra.nat.uni-magdeburg.de/packing/crt/crt.html|title=The best known packings of equal circles in an isosceles right triangle|first=Eckard|last=Specht|date=2011-03-11|accessdate=2011-05-01}}
2. ^{{Cite journal | last1 = Xu | first1 = Y. | title = On the minimum distance determined by n (≤ 7) points in an isoscele right triangle | doi = 10.1007/BF02007736 | journal = Acta Mathematicae Applicatae Sinica | volume = 12 | issue = 2 | pages = 169–175 | year = 1996 | pmid = | pmc = }}
3. ^{{Cite journal | last1 = López | first1 = C. O. | last2 = Beasley | first2 = J. E. | title = A heuristic for the circle packing problem with a variety of containers | doi = 10.1016/j.ejor.2011.04.024 | journal = European Journal of Operational Research | volume = 214 | issue = 3 | pages = 512 | year = 2011 | pmid = | pmc = }}
{{Packing problem}}{{elementary-geometry-stub}}2. ^{{Cite journal | last1 = Xu | first1 = Y. | title = On the minimum distance determined by n (≤ 7) points in an isoscele right triangle | doi = 10.1007/BF02007736 | journal = Acta Mathematicae Applicatae Sinica | volume = 12 | issue = 2 | pages = 169–175 | year = 1996 | pmid = | pmc = }}
3. ^{{Cite journal | last1 = López | first1 = C. O. | last2 = Beasley | first2 = J. E. | title = A heuristic for the circle packing problem with a variety of containers | doi = 10.1016/j.ejor.2011.04.024 | journal = European Journal of Operational Research | volume = 214 | issue = 3 | pages = 512 | year = 2011 | pmid = | pmc = }}
1 : Circle packing
- Rock Run (disambiguation)
- Rock Run (Potomac River tributary)
- Rock Salt & Nails (disambiguation)
- Rock samphire
- Rocksand
- Rocks and Co
- Rock Savage
- Rocksavage
- Rocksavage Hall
- Rocksavage Power Station
- Rocksborough, Ontario
- Rocksborough Smith
- Rocksbury Township, Minnesota
- Rockschool
- Rock scissors
- Rock-scissors-paper
- Rocks & Co.
- Rocks & Co 1
- Rock scorpion books
- Rock Scorpion Books
- Rock Sea Lavender
- Rock sea-lavender
- Rock Sea-lavender
- Rocks (Harem Scarem album)
- Rockshelter