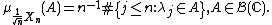“Circular law”的意思、由来-开放百科全书

In probability theory, more specifically the study of random matrices, the circular law concerns the distribution of eigenvalues of an {{math|n × n}} random matrix with independent and identically distributed entries in the limit

It asserts that for any sequence of random {{math|n × n}} matrices whose entries are independent and identically distributed random variables, all with mean zero and variance equal to {{math|1/n}}, the limiting spectral distribution is the uniform distribution over the unit disc.

Precise statement

Let

be a sequence of {{math|n × n}} matrix ensembles whose entries are i.i.d. copies of a complex random variable {{math|x}} with mean 0 and variance 1. Let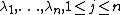

denote the eigenvalues of

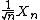. Define the empirical spectral measure of

With these definitions in mind, the circular law asserts that almost surely (i.e. with probability one), the sequence of measures

converges in distribution to the uniform measure on the unit disk.

History

For random matrices with Gaussian distribution of entries (the Ginibre ensembles), the circular law was established in the 1960s by Jean Ginibre.^[1] In the 1980s, Vyacheslav Girko introduced^[2] an approach which allowed to establish the circular law for more general distributions. Further progress was made^[3] by Zhidong Bai, who established the circular law under certain smoothness assumptions on the distribution.

The assumptions were further relaxed in the works of Terence Tao and Van H. Vu,^[4] Guangming Pan and Wang Zhou,^[5] and Friedrich Götze and Alexander Tikhomirov.^[6] Finally, in 2010 Tao and Vu proved^[7] the circular law under the minimal assumptions stated above.

See also

References

1. ^{{cite journal|last=Ginibre|first=Jean|title=Statistical ensembles of complex, quaternion, and real matrices|journal=J. Math. Phys.|year=1965|volume=6|pages=440–449|doi=10.1063/1.1704292|mr=0173726|bibcode=1965JMP.....6..440G}}
2. ^{{cite journal|last=Girko|first=V.L.|title=The circular law|journal=Teor. Veroyatnost. i Primenen.|year=1984|volume=29|issue=4|pages=669–679}}
3. ^{{cite journal|last=Bai|first=Z.D.|title=Circular law|journal=Annals of Probability|year=1997|volume=25|issue=1|pages=494–529|doi=10.1214/aop/1024404298|mr=1428519}}
4. ^{{cite journal|last=Tao|first=T.|last2=Vu|first2=V.H.|title=Random matrices: the circular law.|journal=Commun. Contemp. Math.|year=2008|volume=10|issue=2|pages=261–307|doi=10.1142/s0219199708002788|mr=2409368|arxiv=0708.2895}}
5. ^{{cite journal|last=Pan|first=G.|last2=Zhou|first2=W.|title=Circular law, extreme singular values and potential theory.|journal=J. Multivariate Anal.|year=2010|volume=101|issue=3|pages=645–656|doi=10.1016/j.jmva.2009.08.005}}
6. ^{{cite journal|last=Götze|first=F.|last2=Tikhomirov|first2=A.|title=The circular law for random matrices|journal=Annals of Probability|year=2010|volume=38|issue=4|pages=1444–1491|doi=10.1214/09-aop522|mr=2663633|arxiv=0709.3995}}
7. ^{{cite journal|last1=Tao|first1=Terence|author1-link=Terence Tao|last2=Vu|first2=Van|author2link=Van Vu|title=Random matrices: Universality of ESD and the Circular Law|others=appendix by Manjunath Krishnapur|journal=Annals of Probability|volume=38|issue=5|year=2010|pages=2023–2065|arxiv=0807.4898|doi=10.1214/10-AOP534|mr=2722794}}