“Cohen–Hewitt factorization theorem”的意思、由来-开放百科全书

词条

Cohen–Hewitt factorization theorem

释义

References

In mathematics, the Cohen–Hewitt factorization theorem states that if is a left module over a Banach algebra with a left approximate unit 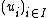, then an element of can be factorized as a product (for some and 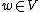) whenever . The theorem was introduced by {{harvs|txt|authorlink=Paul Cohen (mathematician)|last=Cohen|first=Paul|year=1959}} and {{harvs|txt|last=Hewitt|first=Edwin|authorlink=Edwin Hewitt|year=1964}}.

References

{{citation|mr = 0104982

|last = Cohen|first = Paul J.|authorlink = Paul Cohen (mathematician)
|title = Factorization in group algebras
|journal = Duke Mathematical Journal|volume = 26|year = 1959|pages = 199–205|doi = 10.1215/s0012-7094-59-02620-1}}

{{citation|mr = 0187016

|last = Hewitt|first = Edwin|authorlink = Edwin Hewitt
|title = The ranges of certain convolution operators
|journal = Mathematica Scandinavica|volume = 15|year = 1964|pages = 147–155}}{{DEFAULTSORT:Cohen-Hewitt factorization theorem}}{{analysis-stub}}

2 : Banach algebras|Theorems in functional analysis

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。