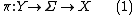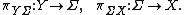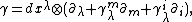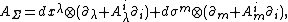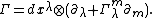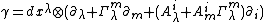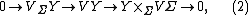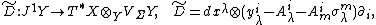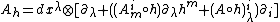“Connection (composite bundle)”的意思、由来-开放百科全书

词条

Connection (composite bundle)

释义

Composite bundle
Composite principal bundle
Jet manifolds of a composite bundle
Composite connection
Vertical covariant differential
References
External links
See also

Composite bundles 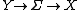play a prominent role in gauge theory with symmetry breaking, e.g., gauge gravitation theory, non-autonomous mechanics where 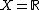is the time axis, e.g., mechanics with time-dependent parameters, and so on. There are the important relations between connections on fiber bundles , 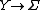and .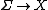

Composite bundle

In differential geometry by a composite bundle is meant the composition

of fiber bundles

It is provided with bundle coordinates 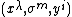, where 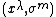are bundle coordinates on a fiber bundle 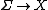, i.e., transition functions of coordinates 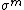are independent of coordinates .

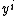The following fact provides the above mentioned physical applications of composite bundles. Given the composite bundle (1), let be a global section

of a fiber bundle 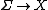, if any. Then the pullback bundle

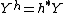over is a subbundle of a fiber bundle .

Composite principal bundle

For instance, let 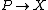be a principal bundle with a structure Lie group which is reducible to its closed subgroup . There is a composite bundl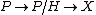e where 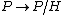is a principal bundle with a structure group and 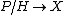is a fiber bundle associated with 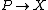. Given a global section of 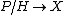, the pullback bundle 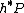is a reduced principal subbundle of with a structure group . In gauge theory, sections of 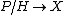are treated as classical Higgs fields.

Jet manifolds of a composite bundle

Given the composite bundle 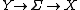(1), let us consider the jet manifolds 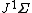, , 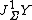and 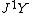of the fiber bundles 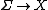, , 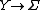and , respectively. They are provided with the adapted coordinates 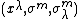, , 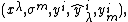and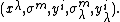

There is the canonical map

.

Composite connection

This canonical map defines the relations between connections on fiber bundles , 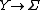and 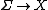. These connections are given by the corresponding tangent-valued connection forms

A connection 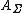on a fiber bundle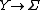

and a connection on a fiber bundle 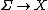define a connection

on a composite bundle . It is called the composite connection. This is a unique connection such that the horizontal lift 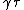onto of a vector field on by means of the composite connection coincides with the composition 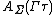of horizontal lifts of onto by means of a connection and then onto by means of a connection .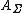

Vertical covariant differential

Given the composite bundle (1), there is the following exact sequence of vector bundles over :

where 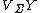and 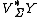are the vertical tangent bundle and the vertical cotangent bundle of 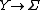. Every connection 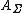on a fiber bundle 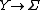yields the splitting

of the exact sequence (2). Using this splitting, one can construct a first order differential operator

on a composite bundle . It is called the vertical covariant differential.

It possesses the following important property.

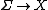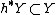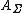Let be a section of a fiber bundle , and let be the pullback bundle over . Every connection induces the pullback connection

on 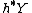. Then the restriction of a vertical covariant differential 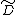to 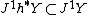coincides with the familiar covariant differential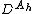

on 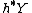relative to the pullback connection .

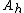References

Saunders, D., The geometry of jet bundles. Cambridge University Press, 1989. {{isbn|0-521-36948-7}}.
Mangiarotti, L., Sardanashvily, G., Connections in Classical and Quantum Field Theory. World Scientific, 2000. {{isbn|981-02-2013-8}}.

External links

Sardanashvily, G., Advanced Differential Geometry for Theoreticians. Fiber bundles, jet manifolds and Lagrangian theory, Lambert Academic Publishing, 2013. {{isbn|978-3-659-37815-7}}; arXiv: 0908.1886