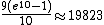- Examples
- Enumeration Estimate for F(n)
- Related problems
- External links
In mathematics a polydivisible number (or magic number) is a number with digits abcde... that has the following properties :
- Its first digit a is not 0.
- The number formed by its first two digits ab is a multiple of 2.
- The number formed by its first three digits abc is a multiple of 3.
- The number formed by its first four digits abcd is a multiple of 4.
- etc.
Examples
For example, 345654 is a six-digit polydivisible number, but 123456 is not, because 1234 is not a multiple of 4. Polydivisible numbers can be defined in any base - however, the numbers in this article are all in base 10, so permitted digits are 0 to 9.
The polydivisible numbers are
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 102, 105, 108, 120, 123, 126, 129, 141, 144, 147, 162, 165, 168, 180, 183, 186, 189, ... {{OEIS|id=A144688}}
The smallest base 10 polydivisible numbers with n digits are
1, 10, 102, 1020, 10200, 102000, 1020005, 10200056, 102000564, 1020005640, 10200056405, 102006162060, 1020061620604, 10200616206046, 102006162060465, 1020061620604656, 10200616206046568, 108054801036000018, 1080548010360000180, 10805480103600001800, ... {{OEIS|id=A214437}}
The largest base 10 polydivisible numbers with n digits are
9, 98, 987, 9876, 98765, 987654, 9876545, 98765456, 987654564, 9876545640, 98765456405, 987606963096, 9876069630960, 98760696309604, 987606963096045, 9876062430364208, 98485872309636009, 984450645096105672, 9812523240364656789, 96685896604836004260, ... {{OEIS|id=A225608}}
Enumeration
The number F(n) of polydivisible numbers of length n for n = 1, 2, 3, ... is
9, 45, 150, 375, 750, 1200, 1713, 2227, 2492, 2492, 2225, 2041, 1575, 1132, 770, 571, 335, 180, 90, 44, 18, 12, 6, 3, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ... {{OEIS|id=A143671}}
There are 20,456 polydivisible numbers altogether, and the longest polydivisible number, which has 25 digits, is
360 852 885 036 840 078 603 672 5
Estimate for F(n)
If k is a polydivisible number with n-1 digits, then it can be extended to create a polydivisible number with n digits if there is a number between 10k and 10k+9 that is divisible by n. If n is less or equal to 10, then it is always possible to extend an n-1 digit polydivisible number to an n-digit polydivisible number in this way, and indeed there may be more than one possible extension. If n is greater than 10, it is not always possible to extend a polydivisible number in this way, and as n becomes larger, the chances of being able to extend a given polydivisible number become smaller. On average, each polydivisible number with n-1 digits can be extended to a polydivisible number with n digits in 10/n different ways. This leads to the following estimate for F(n) :
Summing over all values of n, this estimate suggests that the total number of polydivisible numbers will be approximately
In fact, this underestimates the actual number of polydivisible numbers by about 3%.
| Length n | F(n) | Est. of F(n) |
|---|---|---|
| 1 | 9 | 9 |
| 2 | 45 | 45 |
| 3 | 150 | 150 |
| 4 | 375 | 375 |
| 5 | 750 | 750 |
| 6 | 1200 | 1250 |
| 7 | 1713 | 1786 |
| 8 | 2227 | 2232 |
| 9 | 2492 | 2480 |
| 10 | 2492 | 2480 |
| Length n | F(n) | Est. of F(n) |
|---|---|---|
| 11 | 2225 | 2255 |
| 12 | 2041 | 1879 |
| 13 | 1575 | 1445 |
| 14 | 1132 | 1032 |
| 15 | 770 | 688 |
| 16 | 571 | 430 |
| 17 | 335 | 253 |
| 18 | 180 | 141 |
| 19 | 90 | 74 |
| 20 | 44 | 37 |
| Length n | F(n) | Est. of F(n) |
|---|---|---|
| 21 | 18 | 17 |
| 22 | 12 | 8 |
| 23 | 6 | 3 |
| 24 | 3 | 1 |
| 25 | 1 | 1 |
Related problems
Polydivisible numbers represent a generalization of the following well-known{{citation needed|date=April 2016}} problem in recreational mathematics :
Arrange the digits 1 to 9 in order so that the first two digits form a multiple of 2, the first three digits form a multiple of 3, the first four digits form a multiple of 4 etc. and finally the entire number is a multiple of 9.
The solution to the problem is a nine-digit polydivisible number with the additional condition that it contains the digits 1 to 9 exactly once each. There are 2,492 nine-digit polydivisible numbers, but the only one that satisfies the additional condition is
381 654 729
Other problems involving polydivisible numbers include:
- Finding polydivisible numbers with additional restrictions on the digits - for example, the longest polydivisible number that only uses even digits is
480 006 882 084 660 840 40
- Finding palindromic polydivisible numbers - for example, the longest palindromic polydivisible number is
300 006 000 03
- Enumerating polydivisible numbers in other bases - for example, the longest polydivisible number in base 12 is (using inverted two and three for ten and eleven, respectively)
606 890 346 850 Ɛᘔ6 800 Ɛ03 620 646 4
- A common, trivial extension of the aforementioned example is to arrange the digits 0 to 9 to make a 10 digit number in the same way, the result is 3816547290. This is a pandigital polydivisible number.
External links
- The nine-digit problem and its solution
- Storkówko
- St Orland's Stone
- Storlien
- Storlien railway station
- Storlien station
- Storlien Station
- Storlogen af Danmark
- Storlus
- Storm1
- Storm (1987 film)
- Storm 2
- Storm2
- Storm-333
- Storm 91C
- Storm-Adriance-Brinckerhoff House
- Storm Ahead
- Storm Aircraft Rally
- Stormaktstiden
- Storm (album)
- Stor-Malmo
- Stor-Malmoe
- Stormalong Harbor
- Stormalvatnet
- Storm And Stress
- Stormarn district