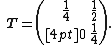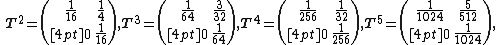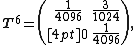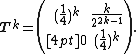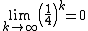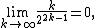“Convergent matrix”的意思、由来-开放百科全书

词条

Convergent matrix

释义

Background
Definition
Example
Characterizations
Iterative methods
Regular splitting
Semi-convergent matrix
See also
Notes
References

In numerical linear algebra, a convergent matrix is a matrix that converges to the zero matrix under matrix exponentiation.

Background

When successive powers of a matrix T become small (that is, when all of the entries of T approach zero, upon raising T to successive powers), the matrix T converges to the zero matrix. A regular splitting of a non-singular matrix A results in a convergent matrix T. A semi-convergent splitting of a matrix A results in a semi-convergent matrix T. A general iterative method converges for every initial vector if T is convergent, and under certain conditions if T is semi-convergent.

Definition

We call an n × n matrix T a convergent matrix if

{{NumBlk|:||{{EquationRef|1}}}}

for each i = 1, 2, ..., n and j = 1, 2, ..., n.^[1]^[2]^[3]

Example

Let

Computing successive powers of T, we obtain

and, in general,

Since

and

T is a convergent matrix. Note that ρ(T) = {{math|{{sfrac|1|4}}}}, where ρ(T) represents the spectral radius of T, since {{math|{{sfrac|1|4}}}} is the only eigenvalue of T.

Characterizations

Let T be an n × n matrix. The following properties are equivalent to T being a convergent matrix:

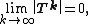for some natural norm;
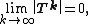for all natural norms;
;
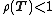for every x.^&91;4&93;^&91;5&93;^&91;6&93;^&91;7&93;

Iterative methods

A general iterative method involves a process that converts the system of linear equations

{{NumBlk|:||{{EquationRef|2}}}}

into an equivalent system of the form

{{NumBlk|:||{{EquationRef|3}}}}

for some matrix T and vector c. After the initial vector x⁽⁰⁾ is selected, the sequence of approximate solution vectors is generated by computing

{{NumBlk|:||{{EquationRef|4}}}}

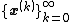for each k ≥ 0.^[8]^[9] For any initial vector x⁽⁰⁾ ∈ , the sequence defined by ({{EquationNote|4}}), for each k ≥ 0 and c ≠ 0, converges to the unique solution of ({{EquationNote|3}}) if and only if ρ(T) < 1, that is, T is a convergent matrix.^[10]^[11]

Regular splitting

A matrix splitting is an expression which represents a given matrix as a sum or difference of matrices. In the system of linear equations ({{EquationNote|2}}) above, with A non-singular, the matrix A can be split, that is, written as a difference

{{NumBlk|:||{{EquationRef|5}}}}

so that ({{EquationNote|2}}) can be re-written as ({{EquationNote|4}}) above. The expression ({{EquationNote|5}}) is a regular splitting of A if and only if B⁻¹ ≥ 0 and C ≥ 0, that is, {{nowrap|B⁻¹}} and C have only nonnegative entries. If the splitting ({{EquationNote|5}}) is a regular splitting of the matrix A and A⁻¹ ≥ 0, then ρ(T) < 1 and T is a convergent matrix. Hence the method ({{EquationNote|4}}) converges.^[12]^[13]

Semi-convergent matrix

We call an n × n matrix T a semi-convergent matrix if the limit

{{NumBlk|:||{{EquationRef|6}}}}

exists.^[14] If A is possibly singular but ({{EquationNote|2}}) is consistent, that is, b is in the range of A, then the sequence defined by ({{EquationNote|4}}) converges to a solution to ({{EquationNote|2}}) for every x⁽⁰⁾ ∈ if and only if T is semi-convergent. In this case, the splitting ({{EquationNote|5}}) is called a semi-convergent splitting of A.^[15]

Notes

1. ^{{harvtxt|Burden|Faires|1993|p=404}}
2. ^{{harvtxt|Isaacson|Keller|1994|p=14}}
3. ^{{harvtxt|Varga|1962|p=13}}
4. ^{{harvtxt|Burden|Faires|1993|p=404}}
5. ^{{harvtxt|Isaacson|Keller|1994|pp=14,63}}
6. ^{{harvtxt|Varga|1960|p=122}}
7. ^{{harvtxt|Varga|1962|p=13}}
8. ^{{harvtxt|Burden|Faires|1993|p=406}}
9. ^{{harvtxt|Varga|1962|p=61}}
10. ^{{harvtxt|Burden|Faires|1993|p=412}}
11. ^{{harvtxt|Isaacson|Keller|1994|pp=62–63}}
12. ^{{harvtxt|Varga|1960|pp=122–123}}
13. ^{{harvtxt|Varga|1962|p=89}}
14. ^{{harvtxt|Meyer & Plemmons|1977|p=699}}
15. ^{{harvtxt|Meyer & Plemmons|1977|p=700}}

References

{{ citation | first1 = Richard L. | last1 = Burden | first2 = J. Douglas | last2 = Faires | year = 1993 | isbn = 0-534-93219-3 | title = Numerical Analysis | edition = 5th | publisher = Prindle, Weber and Schmidt | location = Boston }}.
{{ citation | first1 = Eugene | last1 = Isaacson | first2 = Herbert Bishop | last2 = Keller| year = 1994 | isbn = 0-486-68029-0 | title = Analysis of Numerical Methods | publisher = Dover | location = New York }}.
{{ cite journal | title = Convergent Powers of a Matrix with Applications to Iterative Methods for Singular Linear Systems |date=Sep 1977 | author1 = Carl D. Meyer, Jr. | author2 = R. J. Plemmons | journal = SIAM Journal on Numerical Analysis | volume = 14 | issue = 4 | pages = 699–705 | doi=10.1137/0714047 | ref = {{harvid|Meyer & Plemmons|1977}} }}
{{ Cite book | first1 = Richard S. | last1 = Varga | chapter = Factorization and Normalized Iterative Methods | title = Boundary Problems in Differential Equations | editor1-last = Langer | editor1-first = Rudolph E. | publisher = University of Wisconsin Press | location = Madison | pages = 121–142 | year = 1960 | lccn = 60-60003 | ref = {{harvid|Varga|1960}} }}
{{ citation | first1 = Richard S. | last1 = Varga | title = Matrix Iterative Analysis | publisher = Prentice–Hall | location = New Jersey | year = 1962 | lccn = 62-21277 }}.

4 : Limits (mathematics)|Matrices|Numerical linear algebra|Relaxation (iterative methods)

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。