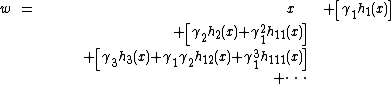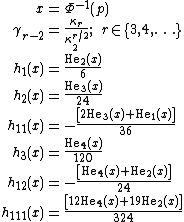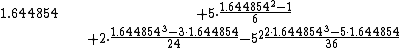“Cornish–Fisher expansion”的意思、由来-开放百科全书

The Cornish–Fisher expansion is an asymptotic expansion used to approximate the quantiles of a probability distribution based on its cumulants.^[1]^[2]^[3]^[4]

It is named after E. A. Cornish and R. A. Fisher, who first described the technique in 1937.^[1]

Definition

For a random variable X with mean μ, variance σ², and cumulants κ_n, its value y_p at quantile p can be estimated as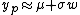

where:^[3]

where He_n is the n^th probabilists' Hermite polynomial. The values γ₁ and γ₂ are the random variable's skewness and (excess) kurtosis respectively. The value(s) in each set of brackets are the terms for that level of polynomial estimation, and all must be calculated and combined for the Cornish–Fisher expansion at that level to be valid.

Example

Let X be a random variable with mean 10, variance 25, skew 5, and excess kurtosis of 2. We can use the first two bracketed terms above, which depend only on skew and kurtosis, to estimate quantiles of this random variable. For the 95th percentile, the value for which the standard normal cumulative distribution function is 0.95 is 1.644854, which will be x. The w weight can be calculated as:

or about 2.55621. So the estimated 95th percentile of X is 10 + 5×2.55621 or about 22.781. For comparison, the 95th percentile of a normal random variable with mean 10 and variance 25 would be about 18.224; it makes sense that the normal random variable has a lower 95th percentile value, as the normal distribution has no skew or excess kurtosis, and so has a thinner tail than the random variable X.

References

1. ^¹{{cite journal| last = Cornish| first = E. A.| last2 = Fisher| first2 = Ronald A.| authorlink2= Ronald Fisher| year = 1938| title = Moments and Cumulants in the Specification of Distributions| journal = Revue de l'Institut International de Statistique / Review of the International Statistical Institute| volume = 5| issue = 4| pages = 307–320| doi = 10.2307/1400905| jstor = 1400905}}
2. ^{{cite journal| last = Fisher| first = Ronald A.| authorlink = Ronald Fisher| last2 = Cornish| first2 = E. A.| year = 1960| title = The Percentile Points of Distributions Having Known Cumulants| journal = Technometrics| volume = 2| issue = 2| pages = 209–225| doi = 10.2307/1266546| jstor = 1266546}}
3. ^¹{{cite book| last1 = Abramowitz| first1 = Milton| author-link1 = Milton Abramowitz| last2 = Stegun| first2 = Irene| author-link2 = Irene Stegun| year = 1964| chapter = 26. Probability Functions| title = Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables| publisher = Dover Publications| page = 935| chapter-url = http://people.math.sfu.ca/~cbm/aands/page_935.htm| accessdate = September 17, 2014| title-link = Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables}}
4. ^{{cite journal| last1 = Martin| first1 = Douglas| last2 = Arora| first2 = Rohit| year = 2017| title = Inefficiency and bias of modified value-at-risk and expected shortfall| journal = Journal of Risk| volume = 19| issue = 6| pages = 59–84| doi = 10.21314/JOR.2017.365}}