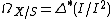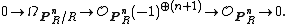“Cotangent sheaf”的意思、由来-开放百科全书

词条

Cotangent sheaf

释义

Construction through a diagonal morphism
Relation to a tautological line bundle
Cotangent stack
Notes
See also
References
External links

In algebraic geometry, given a morphism f: X → S of schemes, the cotangent sheaf on X is the sheaf of -modules that represents (or classifies) S-derivations ^[1] in the sense: for any -modules F, there is an isomorphism

that depends naturally on F. In other words, the cotangent sheaf is characterized by the universal property: there is the differential such that any S-derivation factors as 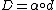with some .

In the case X and S are affine schemes, the above definition means that 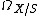is the module of Kähler differentials. The standard way to construct a cotangent sheaf (e.g., Hartshorne, Ch II. § 8) is through a diagonal morphism (which amounts to gluing modules of Kähler differentials on affine charts to get the globally-defined cotangent sheaf.) The dual module of the cotangent sheaf on a scheme X is called the tangent sheaf on X and is sometimes denoted by .^[2]

There are two important exact sequences:

If S →T is a morphism of schemes, then
If Z is a closed subscheme of X with ideal sheaf I, then
^&91;3&93;^&91;4&93;

The cotangent sheaf is closely related to smoothness of a variety or scheme. For example, an algebraic variety is smooth of dimension n if and only if Ω_X is a locally free sheaf of rank n.^[5]

Construction through a diagonal morphism

Let be a morphism of schemes as in the introduction and Δ: X → X ×_S X the diagonal morphism. Then the image of Δ is locally closed; i.e., closed in some open subset W of X ×_S X (the image is closed if and only if f is separated). Let I be the ideal sheaf of Δ(X) in W. One then puts:

and checks this sheaf of modules satisfies the required universal property of a cotangent sheaf (Hartshorne, Ch II. Remark 8.9.2). The construction shows in particular that the cotangent sheaf is quasi-coherent. It is coherent if S is Noetherian and f is of finite type.

The above definition means that the cotangent sheaf on X is the restriction to X of the conormal sheaf to the diagonal embedding of X over S.

Relation to a tautological line bundle

The cotangent sheaf on a projective space is related to the tautological line bundle O(-1) by the following exact sequence: writing for the projective space over a ring R,

(See also Chern class#Complex projective space.)

Cotangent stack

For this notion, see § 1 of

A. Beilinson and V. Drinfeld, Quantization of Hitchin’s integrable system and Hecke eigensheaves ^[6]

There, the cotangent stack on an algebraic stack X is defined as the relative Spec of the symmetric algebra of the tangent sheaf on X. (Note: in general, if E is a locally free sheaf of finite rank, 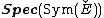is the algebraic vector bundle corresponding to E.)

See also: Hitchin fibration (the cotangent stack of is the total space of the Hitchin fibration.)

Notes

1. ^http://stacks.math.columbia.edu/tag/08RL
2. ^In concise terms, this means::

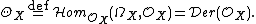
3. ^{{harvnb|Hartshorne|loc=Ch. II, Proposition 8.12.}}
4. ^http://mathoverflow.net/questions/79956/jacobian-criterion-for-smoothness-of-schemes as well as {{harv|Hartshorne|loc=Ch. II, Theorem 8.17.}}
5. ^{{harvnb|Hartshorne|loc=Ch. II, Theorem 8.15.}}
6. ^see also: § 3 of http://www.math.harvard.edu/~gaitsgde/grad_2009/SeminarNotes/Sept22(Dmodstack1).pdf

References

http://stacks.math.columbia.edu/tag/01UM
{{Hartshorne AG}}

External links

http://math.stackexchange.com/questions/1001941/questions-about-tangent-and-cotangent-bundle-on-schemes

1 : Algebraic geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。