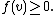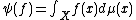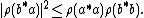“Positive linear functional”的意思、由来-开放百科全书

词条

Positive linear functional

释义

Examples
Positive linear functionals (C*-algebras)
Cauchy–Schwarz inequality
See also
References

In mathematics, more specifically in functional analysis, a positive linear functional on an ordered vector space (V, ≤) is a linear functional f on V so that for all positive elements v of V, that is v≥0, it holds that

In other words, a positive linear functional is guaranteed to take nonnegative values for positive elements. The significance of positive linear functionals lies in results such as Riesz–Markov–Kakutani representation theorem.

When V is a complex vector space, it is assumed that for all v≥0, f(v) is real. As in the case when V is a C*-algebra with its partially ordered subspace of self-adjoint elements, sometimes a partial order is placed on only a subspace W of V, and the partial order does not extend to all of V, in which case the positive elements of V are the positive elements of W, by abuse of notation.{{clarify|Is f(W) ⊆ ℝ further assumed?|date=July 2014}} This implies that for a C*-algebra, a positive linear functional sends any x in V equal to s*s for some s in V to a real number, which is equal to its complex conjugate, and therefore all positive linear functionals preserve the self-adjointness of such x. This property is exploited in the GNS construction to relate positive linear functionals on a C*-algebra to inner products.

Examples

Consider, as an example of V, the C-algebra of complex square matrices with the positive elements being the positive-definite matrices. The trace function defined on this C-algebra is a positive functional, as the eigenvalues of any positive-definite matrix are positive, and so its trace is positive.
Consider the Riesz space C_c(X) of all continuous complex-valued functions of compact support on a locally compact Hausdorff space X. Consider a Borel regular measure μ on X, and a functional ψ defined by

for all f in C_c(X). Then, this functional is positive (the integral of any positive function is a positive number). Moreover, any positive functional on this space has this form, as follows from the Riesz–Markov–Kakutani representation theorem.

Positive linear functionals (C*-algebras)

Let M be a C*-algebra (more generally, an operator system in a C*-algebra A) with identity 1. Let M⁺ denote the set of positive elements in M.

A linear functional ρ on M is said to be positive if ρ(a) ≥ 0, for all a in M⁺.

Theorem. A linear functional ρ on M is positive if and only if ρ is bounded and ||ρ||=ρ(1).^[1]

Cauchy–Schwarz inequality

If ρ is a positive linear functional on a C*-algebra A, then one may define a semidefinite sesquilinear form on A by <a, b> := ρ(b^*a). Thus from the Cauchy–Schwarz inequality we have

References

1. ^{{cite book|last=Murphy|first=Gerard |title=C*-Algebras and Operator Theory|date= |publisher=Academic Press, Inc.|location=|isbn=978-0125113601|edition=1st|chapter=3.3.4|pages=89}}

Kadison, Richard, Fundamentals of the Theory of Operator Algebras, Vol. I : Elementary Theory, American Mathematical Society. {{ISBN|978-0821808191}}.

1 : Functional analysis

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Examples

Positive linear functionals (C*-algebras)

Cauchy–Schwarz inequality

See also

References