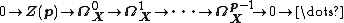“Deligne cohomology”的意思、由来-开放百科全书

词条

Deligne cohomology

释义

Definition
Properties
Applications
References

In mathematics, Deligne cohomology is the hypercohomology of the Deligne complex of a complex manifold. It was introduced by Pierre Deligne in unpublished work in about 1972 as a cohomology theory for algebraic varieties that includes both ordinary cohomology and intermediate Jacobians.

For introductory accounts of Deligne cohomology see {{harvtxt|Brylinski|2008|loc=section 1.5}}, {{harvtxt|Esnault|Viehweg|1988}}, and {{harvtxt|Gomi|2009|loc=section 2}}.

Definition

The analytic Deligne complex Z(p)_{D, an} on a complex analytic manifold X is

where Z(p) = (2π i)^pZ. Depending on the context, 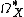is either the complex of smooth (i.e., C^∞) differential forms or of holomorphic forms, respectively.

The Deligne cohomology {{nowrap|{{SubSup|H|D,an|q}}(X,Z(p))}} is the q-th hypercohomology of the Deligne complex.

Properties

Deligne cohomology groups {{nowrap|{{SubSup|H|D|q}}(X,Z(p))}} can be described geometrically, especially in low degrees. For p = 0, it agrees with the q-th singular cohomology group (with Z-coefficients), by definition. For q = 2 and p = 1, it is isomorphic to the group of isomorphism classes of smooth (or holomorphic, depending on the context) principal C^×-bundles over X. For p = q = 2, it is the group of isomorphism classes of C^×-bundles with connection. For q = 3 and p = 2 or 3, descriptions in terms of gerbes are available ({{harvtxt|Brylinski|2008}}). This has been generalized to a description in higher degrees in terms of iterated classifying spaces and connections on them ({{harvtxt|Gajer|1997}}).

Applications

Deligne cohomology is used to formulate Beilinson conjectures on special values of L-functions.

References

{{Citation | last1=Brylinski | first1=Jean-Luc | title=Loop spaces, characteristic classes and geometric quantization | origyear=1993 | publisher=Birkhäuser Boston | location=Boston, MA | series=Modern Birkhäuser Classics | isbn=978-0-8176-4730-8 | doi=10.1007/978-0-8176-4731-5 | mr=2362847 | year=2008}}
{{Citation | last1=Esnault | first1=Hélène | last2=Viehweg | first2=Eckart | title=Beĭlinson's conjectures on special values of L-functions | url=https://books.google.com/books?id=CwTvAAAAMAAJ | publisher=Academic Press | location=Boston, MA | series=Perspect. Math. | mr=944991 | year=1988 | volume=4 | chapter=Deligne-Beĭlinson cohomology | chapterurl=http://www.uni-due.de/~mat903/preprints/ec/deligne_beilinson.pdf | pages=43–91 | isbn=978-0-12-581120-0}}
{{Citation | last1=Gajer | first1=Pawel | title=Geometry of Deligne cohomology | doi=10.1007/s002220050118 | year=1997 | journal=Inventiones Mathematicae | issn=0020-9910 | volume=127 | issue=1 | pages=155–207| arxiv=alg-geom/9601025 | bibcode=1996InMat.127..155G }}
{{Citation | last1=Gomi | first1=Kiyonori | title=Projective unitary representations of smooth Deligne cohomology groups | doi=10.1016/j.geomphys.2009.06.012 | mr=2541824 | year=2009 | journal=Journal of Geometry and Physics | issn=0393-0440 | volume=59 | issue=9 | pages=1339–1356 | arxiv=math/0510187| bibcode=2009JGP....59.1339G }}

3 : Sheaf theory|Homological algebra|Cohomology theories

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。