“Derivative-free optimization”的意思、由来-开放百科全书

词条

Derivative-free optimization

释义

Introduction
Algorithms
Software
See also
References

Derivative-free optimization is a discipline in mathematical optimization that does not use derivative information in the classical sense to find optimal solutions: Sometimes information about the derivative of the objective function f is unavailable, unreliable or impractical to obtain. For example, f might be non-smooth, or time-consuming to evaluate, or in some way noisy, so that methods that rely on derivatives or approximate them via finite differences are of little use. The problem to find optimal points in such situations is referred to as derivative-free optimization, algorithms that do not use derivatives or finite differences are called derivative-free algorithms (note that this classification is not precise).^[1]

Derivative-free optimization is closely related to black-box optimization.^[2]

Introduction

The problem to be solved is to numerically optimize an objective function 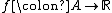for some set (usually 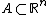), i.e. find 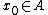such that without loss of generality 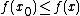for all .

When applicable, a common approach is to iteratively improve a parameter guess by local hill-climbing in the objective function landscape. Derivative-based algorithms use derivative information of to find a good search direction, since for example the gradient gives the direction of steepest ascent. Derivative-based optimization is efficient at finding local optima for continuous-domain smooth single-modal problems. However, they can have problems when e.g. is disconnected, or (mixed-)integer, or when is expensive to evaluate, or is non-smooth, or noisy, so that (numeric approximations of) derivatives do not provide useful information. A slightly different problem is when is multi-modal, in which case local derivative-based methods only give local optima, but might miss the global one.

In derivative-free optimization, various methods are employed to address these challenges using only function values of , but no derivatives. Some of these methods can be proved to discover optima, but some are rather metaheuristic since the problems are in general more difficult to solve compared to convex optimization. For these, the ambition is rather to efficiently find "good" parameter values which can be near-optimal given enough resources, but optimality guarantees can typically not be given. One should keep in mind that the challenges are diverse, so that one can usually not use one algorithm for all kinds of problems.

Algorithms

A non-exhaustive collection of derivative-free optimization algorithms follows:

DONE
Bayesian optimization
Coordinate descent and adaptive coordinate descent
Cuckoo search
Evolution strategies, Natural evolution strategies (CMA-ES, xNES, SNES)
Cross-entropy methods (CEM)
Genetic algorithms
LIPO algorithm
MCS algorithm
Nelder-Mead method
Particle swarm optimization
Pattern search
Powell's COBYLA, UOBYQA, NEWUOA, BOBYQA and LINCOA algorithms
Random search (including Luus-Jaakola)
Shuffled complex evolution algorithm
Simulated annealing
Subgradient method

Software

Of the algorithms referred to above, there exist various established implementations either stand-alone or in toolboxes, for example:

SciPy: Includes Nelder–Mead_method, several by Powell, Differential_evolution, and several others. Several algorithms that use derivatives can analytically estimate the derivative, including L-BFGS, SLSQP, CG.
[https://nlopt.readthedocs.io/en/latest/ NLOpt library for nonlinear optimization]: Includes Brent's Praxis, Controlled Random Search, several by Powell (COBYLA, NEWUOA, BOBYQA), and the Nelder–Mead_method.
CMA-ES (Covariance Matrix Adaptation Evolution Strategy)
[https://github.com/avaneev/biteopt BiteOpt derivative-free stochastic optimization method] at GitHub
[https://www.mathworks.com/products/global-optimization.html Matlab Global Optimization Toolbox]: Includes several implementations of derivative-free algorithms
MEIGO: Several meta-heuristic methods for continuous and (mixed-)integer problems
[https://github.com/icb-dcm/pesto PESTO]: A parameter optimization toolbox including also various derivative-free methods
PSWARM: A particle swarm implementation
[https://github.com/facebookresearch/nevergrad nevergrad]: A gradient-free optimization platform based on python3. Various algorithms, tools, functions and benchmark routines are available.

A comprehensive evaluation of various implementations can be found at.^[3]

References

1. ^{{cite book|last=Conn |first=A. R. |last2=Scheinberg |first2=K.|author2-link= Katya Scheinberg |last3=Vicente |first3=L. N. |year=2009 |title=Introduction to Derivative-Free Optimization |url=http://www.mat.uc.pt/~lnv/idfo/|accessdate=2014-01-18 |series= MPS-SIAM Book Series on Optimization| publisher=SIAM|location=Philadelphia}}
2. ^{{cite journal |last=Audet |first=Charles |last2=Kokkolaras |first2=Michael |year=2016 |title=Blackbox and derivative-free optimization: theory, algorithms and applications |journal=Optimization and Engineering |volume=17 |pages=1–2 |doi=10.1007/s11081-016-9307-4 }}
3. ^{{cite journal |last=Rios |first=LM |last2=Sahinidis |first2=NV |year=2013 |title=Derivative-free optimization: a review of algorithms and comparison of software implementations |journal=Journal of Global Optimization |volume=56 |issue=3 |pages=1247–1293 |doi=10.1007/s10898-012-9951-y }}

1 : Optimization algorithms and methods

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Introduction

Algorithms

Software

See also

References