“De-sparsified lasso”的意思、由来-开放百科全书

词条

De-sparsified lasso

释义

1 High-dimensional linear model
2 Generalized linear model
References

{{Orphan|date=July 2016}}{{Expert needed|Mathematics|reason=needs a better lead and overview, more general context and categorization|date=June 2015}}De-sparsified lasso contributes to construct confidence intervals and statistical tests for single or low-dimensional components of a large parameter vector in high-dimensional model.^[1]

1 High-dimensional linear model

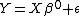
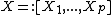with design matrix ( vectors ), 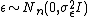independent of and unknown regression 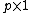vector .

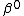The usual method to find the parameter is by Lasso:

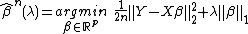
The de-sparsified lasso is a method modified from the Lasso estimator which fulfills the Karush-Kuhn-Tucker conditions^[2] is as follows:

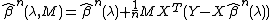
where 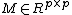is an arbitrary matrix. The matrix is generated using a surrogate inverse covariance matrix.

2 Generalized linear model

Desparsifying -norm penalized estimators and corresponding theory can also be applied to models with convex loss functions such as generalized linear models.

Consider the following 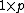vectors of covariables 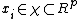and univariate responses for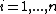

we have a loss function

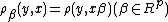
which is assumed to be strictly convex function in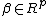

The -norm regularized estimator is

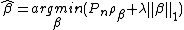
Similarly, the Lasso for node wise regression with matrix input is defined as follows:

Denote by 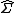a matrix which we want to approximately invert using nodewise lasso.

The de-sparsified -norm regularized estimator is as follows:

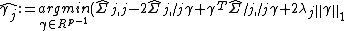
where 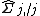denotes the th row of 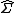without the diagonal element 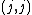, and 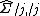is the sub matrix without the th row and th column.

References

1. ^{{cite journal|last1=GEER|first1=SARA VAN DE|last2=BUHLMANN|first2=PETER|last3=RITOV|first3=YA' ACOV|last4=DEZEURE|first4=RUBEN|title=ON ASYMPTOTICALLY OPTIMAL CONFIDENCE REGIONS AND TESTS FOR HIGH-DIMENSIONAL MODELS|journal=The Annals of Statistics|date=2014|volume=42|pages=1162–1202|doi=10.1214/14-AOS1221|arxiv=1303.0518}}
2. ^{{cite web|last1=Tibshirani|first1=Ryan|last2=Gordon|first2=Geoff|title=Karush-Kuhn-Tucker conditions|url=https://www.cs.cmu.edu/~ggordon/10725-F12/slides/16-kkt.pdf}}

1 : Generalized linear models

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。