“Dieudonné's theorem”的意思、由来-开放百科全书

词条

Dieudonné's theorem

释义

Statement of theorem
References

In mathematics, Dieudonné's theorem, named after Jean Dieudonné, is a theorem on when the Minkowski sum of closed sets is closed.

Statement of theorem

Let nonempty closed convex sets 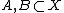a locally convex space, if either or is locally compact and 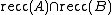(where 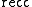gives the recession cone) is a linear subspace, then 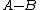is closed.^[1]^[2]

References

1. ^{{cite journal|title=Sur la séparation des ensembles convexes|author=J. Dieudonné|year=1966|journal=Math. Ann.|volume=163}}
2. ^{{cite book |last=Zălinescu |first=Constantin |title=Convex analysis in general vector spaces |publisher=World Scientific Publishing Co., Inc. |isbn=981-238-067-1 |mr=1921556 |issue=J |year=2002 |location=River Edge, NJ |pages=6–7}}

2 : Convex analysis|Theorems in functional analysis

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。