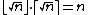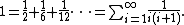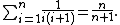“Pronic number”的意思、由来-开放百科全书

A pronic number is a number which is the product of two consecutive integers, that is, a number of the form {{math|n(n + 1)}}.^[1] The study of these numbers dates back to Aristotle. They are also called oblong numbers, heteromecic numbers,^[2] or rectangular numbers;^[3] however, the "rectangular number" name has also been applied to the composite numbers.^[3]^[4]

As figurate numbers

The pronic numbers were studied as figurate numbers alongside the triangular numbers and square numbers in Aristotle's Metaphysics,^[2] and their discovery has been attributed much earlier to the Pythagoreans.^[5]

As a kind of figurate number, the pronic numbers are sometimes called oblong^[2] because they are analogous to polygonal numbers in this way:^[1]

The {{mvar|n}}th pronic number is twice the {{mvar|n}}th triangular number^[1]^[2] and {{mvar|n}} more than the {{mvar|n}}th square number, as given by the alternative formula {{math|n² + n}} for pronic numbers. The {{mvar|n}}th pronic number is also the difference between the odd square {{math|(2n + 1)²}} and the {{math|(n+1)}}st centered hexagonal number.

Sum of pronic numbers

The sum of the reciprocals of the pronic numbers (excluding 0) is a telescoping series that sums to 1:^[6]

The partial sum of the first {{mvar|n}} pronic numbers is twice the value of the {{mvar|n}}th tetrahedral number:

Additional properties

The {{mvar|n}}th pronic number is the sum of the first {{mvar|n}} even integers.^[2]

It follows that all pronic numbers are even, and that 2 is the only prime pronic number. It is also the only pronic number in the Fibonacci sequence and the only pronic Lucas number.^[7]^[8]

The number of off-diagonal entries in a square matrix is always a pronic number.^[9]

The fact that consecutive integers are coprime and that a pronic number is the product of two consecutive integers leads to a number of properties. Each distinct prime factor of a pronic number is present in only one of the factors n or n+1. Thus a pronic number is squarefree if and only if {{mvar|n}} and {{math|n + 1}} are also squarefree. The number of distinct prime factors of a pronic number is the sum of the number of distinct prime factors of {{mvar|n}} and {{math|n + 1}}.

If 25 is appended to the decimal representation of any pronic number, the result is a square number e.g. 625 = 25², 1225 = 35². This is because

References

1. ^¹²{{citation |first1=J. H. |last1=Conway |author1-link=John H. Conway |first2=R. K. |last2=Guy |author2-link=Richard K. Guy |title=The Book of Numbers |location=New York |publisher=Copernicus |at=Figure 2.15, p. 34 |year=1996}}.
2. ^¹²³⁴{{citation | last = Knorr | first = Wilbur Richard | author-link = Wilbur Knorr | isbn = 90-277-0509-7 | location = Dordrecht-Boston, Mass. | mr = 0472300 | pages = 144–150 | publisher = D. Reidel Publishing Co. | title = The evolution of the Euclidean elements | url = https://books.google.com/books?id=_1H6BwAAQBAJ&pg=PA144 | year = 1975}}.
3. ^{{cite web|url=http://www.perseus.tufts.edu/hopper/text?doc=Perseus:text:2008.01.0238:section=42|title=Plutarch, De Iside et Osiride, section 42|author=|date=|website=www.perseus.tufts.edu|accessdate=16 April 2018}}
4. ^{{citation|title=Number Story: From Counting to Cryptography|first=Peter Michael|last=Higgins|publisher=Copernicus Books|year=2008|isbn=9781848000018|page=9|url=https://books.google.com/books?id=HcIwkWXy3CwC&pg=PA9}}.
5. ^¹{{citation|title=Historical Encyclopedia of Natural and Mathematical Sciences, Volume 1|series=Springer reference|first=Ari|last=Ben-Menahem|publisher=Springer-Verlag|year=2009|isbn=9783540688310|page=161|url=https://books.google.com/books?id=9tUrarQYhKMC&pg=PA161}}.
6. ^¹{{citation|title=The Calculus Collection: A Resource for AP and Beyond|series=Classroom Resource Materials|editor1-first=Caren L.|editor1-last=Diefenderfer|editor2-first=Roger B.|editor2-last=Nelsen|publisher=Mathematical Association of America|year=2010|isbn=9780883857618|pages=467–468|contribution-url=https://books.google.com/books?id=SHJ39945R1kC&pg=PA467|contribution=The telescoping series in perspective|first=Marc|last=Frantz}}.
7. ^{{citation | last = McDaniel | first = Wayne L. | issue = 1 | journal = Fibonacci Quarterly | mr = 1605345 | pages = 60–62 | title = Pronic Lucas numbers | url = http://www.mathstat.dal.ca/FQ/Scanned/36-1/mcdaniel2.pdf | volume = 36 | year = 1998}}.
8. ^{{citation | last = McDaniel | first = Wayne L. | issue = 1 | journal = Fibonacci Quarterly | mr = 1605341 | pages = 56–59 | title = Pronic Fibonacci numbers | url = http://www.fq.math.ca/Scanned/36-1/mcdaniel1.pdf | volume = 36 | year = 1998}}.
9. ^{{citation|title=Applied Factor Analysis|first=Rudolf J.|last=Rummel|publisher=Northwestern University Press|year=1988|isbn=9780810108240|page=319|url=https://books.google.com/books?id=g_eNa_XzyEIC&pg=PA319}}.