请输入您要查询的百科知识：

　

词条 Proper morphism
释义

  1. Definition

  2. Examples

  3. Properties and characterizations of proper morphisms

      Valuative criterion of properness  

  4. Proper morphism of formal schemes

  5. See also

  6. References

  7. External links

In algebraic geometry, a proper morphism between schemes is an analog of a proper map between complex analytic spaces.

Some authors call a proper variety over a field k a complete variety. For example, every projective variety over a field k is proper over k. A scheme X of finite type over the complex numbers (for example, a variety) is proper over C if and only if the space X(C) of complex points with the classical (Euclidean) topology is compact and Hausdorff.

A closed immersion is proper. A morphism is finite if and only if it is proper and quasi-finite.

Definition

A morphism f: X → Y of schemes is called universally closed if for every scheme Z with a morphism Z → Y, the projection from the fiber product

is a closed map of the underlying topological spaces. A morphism of schemes is called proper if it is separated, of finite type, and universally closed ([EGA] II, 5.4.1 [https://web.archive.org/web/20051108184937/http://modular.fas.harvard.edu/scans/papers/grothendieck/PMIHES_1961__8__5_0.pdf]). One also says that X is proper over Y. In particular, a variety X over a field k is said to be proper over k if the morphism X → Spec(k) is proper.

Examples

For any natural number n, projective space Pn over a commutative ring R is proper over R. Projective morphisms are proper, but not all proper morphisms are projective. For example, there is a smooth proper complex variety of dimension 3 which is not projective over C.[1] Affine varieties of positive dimension over a field k are never proper over k. More generally, a proper affine morphism of schemes must be finite.[2] For example, it is not hard to see that the affine line A1 over a field k is not proper over k, because the morphism A1 → Spec(k) is not universally closed. Indeed, the pulled-back morphism

(given by (x,y) ↦ y) is not closed, because the image of the closed subset xy = 1 in A1 × A1 = A2 is A1 − 0, which is not closed in A1.

Properties and characterizations of proper morphisms

In the following, let f: X → Y be a morphism of schemes.

  • The composition of two proper morphisms is proper.
  • Any base change of a proper morphism f: X → Y is proper. That is, if g: Z → Y is any morphism of schemes, then the resulting morphism X ×Y Z → Z is proper.
  • Properness is a local property on the base (in the Zariski topology). That is, if Y is covered by some open subschemes Yi and the restriction of f to all f−1(Yi) is proper, then so is f.
  • More strongly, properness is local on the base in the fpqc topology. For example, if X is a scheme over a field k and E is a field extension of k, then X is proper over k if and only if the base change XE is proper over E.[3]
  • Closed immersions are proper.
  • More generally, finite morphisms are proper. This is a consequence of the going up theorem.
  • By Deligne, a morphism of schemes is finite if and only if it is proper and quasi-finite.[4] This had been shown by Grothendieck if the morphism f: X → Y is locally of finite presentation, which follows from the other assumptions if Y is noetherian.[5]
  • For X proper over a scheme S, and Y separated over S, the image of any morphism X → Y over S is a closed subset of Y.[6] This is analogous to the theorem in topology that the image of a continuous map from a compact space to a Hausdorff space is a closed subset.
  • The Stein factorization theorem states that any proper morphism to a locally noetherian scheme can be factored as X → Z → Y, where X → Z is proper, surjective, and has geometrically connected fibers, and Z → Y is finite.[7]
  • Chow's lemma says that proper morphisms are closely related to projective morphisms. One version is: if X is proper over a quasi-compact scheme Y and X has only finitely many irreducible components (which is automatic for Y noetherian), then there is a projective surjective morphism g: W → X such that W is projective over Y. Moreover, one can arrange that g is an isomorphism over a dense open subset U of X, and that g−1(U) is dense in W. One can also arrange that W is integral if X is integral.[8]
  • Nagata's compactification theorem, as generalized by Deligne, says that a separated morphism of finite type between quasi-compact and quasi-separated schemes factors as an open immersion followed by a proper morphism.[9]
  • Proper morphisms between locally noetherian schemes preserve coherent sheaves, in the sense that the higher direct images Rif∗(F) (in particular the direct image f∗(F)) of a coherent sheaf F are coherent (EGA III, 3.2.1). (Analogously, for a proper map between complex analytic spaces, Grauert and Remmert showed that the higher direct images preserve coherent analytic sheaves.) As a very special case: the ring of regular functions on a proper scheme X over a field k has finite dimension as a k-vector space. By contrast, the ring of regular functions on the affine line over k is the polynomial ring k[x], which does not have finite dimension as a k-vector space.
  • There is also a slightly stronger statement of this:{{harv|EGA III|loc=3.2.4}} let be a morphism of finite type, S locally noetherian and a -module. If the support of F is proper over S, then for each 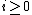the higher direct image 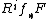is coherent.
  • For a scheme X of finite type over the complex numbers, the set X(C) of complex points is a complex analytic space, using the classical (Euclidean) topology. For X and Y separated and of finite type over C, a morphism f: X → Y over C is proper if and only if the continuous map f: X(C) → Y(C) is proper in the sense that the inverse image of every compact set is compact.[10]
  • If f: X→Y and g: Y→Z are such that gf is proper and g is separated, then f is proper. This can for example be easily proven using the following criterion.

Valuative criterion of properness

Similarly, f is separated if and only if in every such diagram, there is at most one lift .

For example, given the valuative criterion, it becomes easy to check that projective space Pn is proper over a field (or even over Z). One simply observes that for a discrete valuation ring R with fraction field K, every K-point [x0,...,xn] of projective space comes from an R-point, by scaling the coordinates so that all lie in R and at least one is a unit in R.

Proper morphism of formal schemes

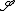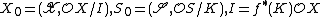Let be a morphism between locally noetherian formal schemes. We say f is proper or is proper over if (i) f is an adic morphism (i.e., maps the ideal of definition to the ideal of definition) and (ii) the induced map is proper, where and K is the ideal of definition of 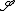.{{harv|EGA III|loc=3.4.1}} The definition is independent of the choice of K.

For example, if g: Y → Z is a proper morphism of locally noetherian schemes, Z0 is a closed subset of Z, and Y0 is a closed subset of Y such that g(Y0) ⊂ Z0, then the morphism on formal completions is a proper morphism of formal schemes.

Grothendieck proved the coherence theorem in this setting. Namely, let be a proper morphism of locally noetherian formal schemes. If F is a coherent sheaf on , then the higher direct images 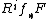are coherent.[11]

See also

  • Proper base change theorem
  • Stein factorization

References

1. ^Hartshorne (1977), Appendix B, Example 3.4.1.
2. ^Liu (2002), Lemma 3.3.17.
3. ^{{Citation | title=Stacks Project, Tag 02YJ | url=http://stacks.math.columbia.edu/tag/02YJ}}.
4. ^Grothendieck, EGA IV, Part 4, Corollaire 18.12.4; {{Citation | title=Stacks Project, Tag 02LQ | url=http://stacks.math.columbia.edu/tag/02LQ}}.
5. ^Grothendieck, EGA IV, Part 3, Théorème 8.11.1.
6. ^{{Citation | title=Stacks Project, Tag 01W0 | url=http://stacks.math.columbia.edu/tag/01W0}}.
7. ^{{Citation | title=Stacks Project, Tag 03GX | url=http://stacks.math.columbia.edu/tag/03GX}}.
8. ^Grothendieck, EGA II, Corollaire 5.6.2.
9. ^Conrad (2007), Theorem 4.1.
10. ^{{harvnb|SGA 1|loc=XII Proposition 3.2.}}
11. ^Grothendieck, EGA III, Part 1, Théorème 3.4.2.
  • {{Citation | author1-last=Conrad | author1-first=Brian | author1-link=Brian Conrad | title=Deligne's notes on Nagata compactifications | journal=Journal of the Ramanujan Mathematical Society | volume=22 | year=2007 | pages=205–257 | mr=2356346 | url=http://math.stanford.edu/~conrad/papers/nagatafinal.pdf}}
  • {{EGA|book=2| pages = 5–222}}, section 5.3. (definition of properness), section 7.3. (valuative criterion of properness)
  • {{EGA|book=3-1| pages = 5–167}}
  • {{EGA|book=4-3| pages = 5–255}}, section 15.7. (generalizations of valuative criteria to not necessarily noetherian schemes)
  • {{EGA|book=4-4| pages = 5–361}}
  • {{Citation | last1=Hartshorne | first1=Robin | author1-link= Robin Hartshorne | title=Algebraic Geometry | publisher=Springer-Verlag | location=Berlin, New York | isbn=978-0-387-90244-9 |mr=0463157 | year=1977}}
  • {{Citation | last=Liu | first=Qing |title=Algebraic geometry and arithmetic curves| publisher=Oxford University Press | location=Oxford | isbn= 9780191547805 | MR=1917232 | year=2002}}

External links

  • {{springer |id=P/p075450|title=Proper morphism|author=V.I. Danilov}}
  • {{Citation | author1=The Stacks Project Authors | title=The Stacks Project | url=http://stacks.math.columbia.edu/}}

1 : Morphisms of schemes
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/10 16:34:38