1. Examples

2. See also

3. References

In mathematics, a pro-p group (for some prime number p) is a profinite group such that for any open normal subgroup the quotient group is a p-group. Note that, as profinite groups are compact, the open subgroups are exactly the closed subgroups of finite index, so that the discrete quotient group is always finite.

Alternatively, one can define a pro-p group to be the inverse limit of an inverse system of discrete finite p-groups.

The best-understood (and historically most important) class of pro-p groups is the p-adic analytic groups: groups with the structure of an analytic manifold over such that group multiplication and inversion are both analytic functions.

The work of Lubotzky and Mann, combined with Michel Lazard's solution to Hilbert's fifth problem over the p-adic numbers, shows that a pro-p group is p-adic analytic if and only if it has finite rank, i.e. there exists a positive integer such that any closed subgroup has a topological generating set with no more than elements. More generally it was shown that a finetly generated profinite group is a compact p-adic Liegroup if and only if it has an open subgroup that is an uniformly powerful pro-p-group.

The Coclass Theorems have been proved in 1994 by A. Shalev and independently by C. R. Leedham-Green. Theorem D is one of these theorems and asserts that, for any prime number p and any positive integer r, there exist only finitely many pro-p groups of coclass r. This finiteness result is fundamental for the classification of finite p-groups by means of directed coclass graphs.

Examples

• The canonical example is the p-adic integers

• The group 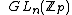of invertible n by n matrices over has an open subgroup U consisting of all matrices congruent to the identity matrix modulo 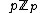. This U is a pro-p group. In fact the p-adic analytic groups mentioned above can all be found as closed subgroups of 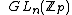for some integer n,
• Any finite p-group is also a pro-p-group (with respect to the constant inverse system).
• Fact: A finite homomorphic image of a pro-p group is a p-group. (due to J.P. Serre)

See also

• Residual property (mathematics)
• Profinite group (See Property or Fact 5)

References

• {{citation |mr=1152800 | last1=Dixon | first1=J. D. | last2=du Sautoy | first2=M. P. F. | last3=Mann | first3=A. | last4=Segal | first4=D. | title=Analytic pro-p-groups | publisher=Cambridge University Press | year=1991 | ISBN=0-521-39580-1 | author2-link=Marcus du Sautoy}}
• {{citation | last1=du Sautoy | first1=M. | last2=Segal | first2=D. | last3=Shalev | first3=A.| title=New Horizons in pro-p Groups | publisher=Birkhäuser | year=2000 | ISBN=0-8176-4171-8}}

• Megachile rufocaudata
• Megachile rufofulva
• Megachile rufohirtula
• Megachile rufolobata
• Megachile rufomaculata
• Megachile rufopilosa
• Megachile rufoscopacaea
• Megachile rufosuffusa
• Megachile rufovittata
• Megachile rufulina
• Megachile rugicollis
• Megachile rugifrons
• Megachile rugosa
• Megachile rupshuensis
• Megachile saba
• Megachile sabinensis
• Megachile saganeitana
• Megachile saigonensis
• Megachile salsburyana
• Megachile sandacana
• Megachile santacrucensis
• Megachile santaerosae
• Megachile santaremensis
• Megachile santiaguensis
• Megachile saulcyi