“Pruning (morphology)”的意思、由来-开放百科全书

词条

Pruning (morphology)

释义

Mathematical Definition
Structuring Elements Step 1: Thinning Step 2: Find End Points Step 3: Dilate End Points Step 4: Union of X₁ & X₃
MATLAB Code
MATLAB Example
See also
External links
References

^[1] The pruning algorithm is a technique used in digital image processing based on mathematical morphology. It is used as a complement to the skeleton and thinning algorithms to remove unwanted parasitic components (spurs). In this case 'parasitic' components refer to branches of a line which are not key to the overall shape of the line and should be removed. These components can often be created by edge detection algorithms or digitization. Common uses for pruning include automatic recognition of hand-printed characters. Often times inconsistency in letter writing create unwanted spurs that need to be eliminated for better characterization.^[2]

Mathematical Definition

The standard pruning algorithm will remove all branches shorter than a given number of points. If a parasitic branch is shorter than four points and we run the algorithm with n = 4 the branch will be removed. The second step ensures that the main trunks of each line are not shortened by the procedure.

Structuring Elements

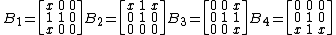
The x in the arrays indicates a “don’t care” condition i.e. the image could have either a 1 or a 0 in the spot.

Step 1: Thinning

Apply this step a given (n) times to eliminate any branch with (n) or less pixels.

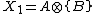
Step 2: Find End Points

Wherever the structuring elements are satisfied, the center of the 3x3 matrix is considered an endpoint.

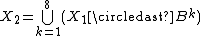
Step 3: Dilate End Points

Perform dilation using a 3x3 matrix (H) consisting of all 1's and only insert 1's where the original image (A) also had a 1. Perform this for each endpoint in all direction (n) times.

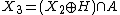
Step 4: Union of X₁ & X₃

Take the result from step 1 and union it with step 3 to achieve the final results.

MATLAB Code

%% ---------------

% Pruning

% ---------------

clear; clc;

% Image read in

img = imread('Pruning.tif');

b_img_skel = bwmorph(img, 'skel', 40);

b_img_spur = bwmorph(b_img_skel, 'spur', Inf);

figure('Name', 'Pruning');

subplot(1,2,1);

imshow(b_img_skel);

title(sprintf('Image Skeleton'));

subplot(1,2,2);

imshow(b_img_spur);

title(sprintf('Skeleton Image Pruned'));

MATLAB Example

In the MATLAB example below, it takes the original image (below left) and skeletonize it 40 times then prunes the image to remove the spurs as per the MATLAB code above. As shown (below right) this removed the majority of all spurs resulting in a cleaner image.

Original Image	Image Skeleton	Skeleton Image Pruned

External links

Morphological Pruning function in Mathematica
[https://www.mathworks.com/help/images/ref/bwmorph.html Morphological Operations] in MATLAB

References

1. ^{{cite book|last1=Russ|first1=John C.|title=The image processing handbook|date=2011|publisher=CRC Press|location=Boca Raton|isbn=978-1-4398-4045-0|edition=6th}}
2. ^{{cite book|title=Digital image processing|last1=Gonzalez|first1=Rafael C.|last2=Woods|first2=Richard E.|date=2008|publisher=Prentice Hall|isbn=978-0131687288|edition=3rd|location=Upper Saddle River, N.J.}}

2 : Digital geometry|Mathematical morphology

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。