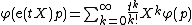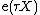“Draft:Lie's formula”的意思、由来-开放百科全书

词条

Draft:Lie's formula

释义

j function

Lie's formula, due to Sophus Lie (1888), says: if {{math|p}} is a point on a real or complex analytic manifold {{math|M}}, {{math|X}} is a analytic vector field, {{math|φ}} an analytic function, then

where on the right X is viewed as a a first order differential operator operating on {{math|φ}}. In other words, it gives the Taylor series of {{math|φ}} along one-parameter subgroup.

Here {{math|X}} is an analytic vector field, and {{math|exp}} is the flow of {{math|X}}, and {{math|τ}} is the "time" of the flow. Its proof depends on {{math|φ}} having a Taylor series. In a smooth manifold setting, the exponential mapping is simply defined to be the time one flow of a (left invariant) smooth vector field without the strong motivational point of the power series for its name.

On the left hand side,

is, for each {{math|τ ∈ R}}, a bi-analytic bijection (the analytic counterpart of diffeomorphism) from the analytic manifold (the Lie group) to itself. Thus

is a new point on the manifold. When {{math|τ}} varies ({{math|p}} fixed), an integral curve of {{math|X}} is obtained. With {{math|p}} = the identity,

can be considered as a one-parameter subgroup as {{math|τ}} varies over all {{math|R}} (provided {{math|X}} is in the Lie algebra). All one-parameter subgroups of the Lie group are expressible as such for some {{math|X}} in the Lie algebra (the left-invariant vector fields ≃ tangent space at the identity).

On the right hand side, {{math|X}} is to be thought of as . Every {{math|X}} in the Lie algebra can canonically be associated with such a differential operator on the whole Lie group. This extends the concept of a Taylor series globally and in a coordinate-independent way.

j function

It is the Jacobian of the exponential map.