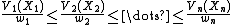- Setting
- Statements
- Corollaries Consensus partition Super-proportional division
- Sketch of Proof Utilitarian-optimal division Leximin-optimal division
- Further developments
- See also
- References
The Dubins–Spanier theorems are several theorems in the theory of fair cake-cutting. They were published by Lester Dubins and Edwin Spanier in 1961.[1] Although the original motivation for these theorems is fair division, they are in fact general theorems in measure theory.
Setting
There is a set  , and a set
, and a set  which is a sigma-algebra of subsets of
which is a sigma-algebra of subsets of  .
.
There are  partners. Every partner
partners. Every partner  has a personal value measure
has a personal value measure 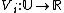 . This function determines how much each subset of
. This function determines how much each subset of  is worth to that partner.
is worth to that partner.
Let  a partition of
a partition of  to
to  measurable sets:
measurable sets: 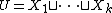 . Define the matrix
. Define the matrix  as the following
as the following  matrix:
matrix:
This matrix contains the valuations of all players to all pieces of the partition.
Let  be the collection of all such matrices (for the same value measures, the same
be the collection of all such matrices (for the same value measures, the same  , and different partitions):
, and different partitions):
The Dubins–Spanier theorems deal with the topological properties of  .
.
Statements
If all value measures  are countably-additive and nonatomic, then:
are countably-additive and nonatomic, then:
-
 is a compact set;
is a compact set; -
 is a convex set.
is a convex set.
This was already proved by Dvoretzky, Wald, and Wolfowitz. [2]
Corollaries
Consensus partition
A cake partition  to k pieces is called a consensus partition with weights
to k pieces is called a consensus partition with weights 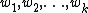 (also called exact division) if:
(also called exact division) if:
I.e, there is a consensus among all partners that the value of piece j is exactly  .
.
Suppose, from now on, that 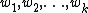 are weights whose sum is 1:
are weights whose sum is 1:
and the value measures are normalized such that each partner values the entire cake as exactly 1:
The convexity part of the DS theorem implies that:[1]{{rp|5}}
If all value measures are countably-additive and nonatomic,
then a consensus partition exists.
PROOF: For every  , define a partition
, define a partition  as follows:
as follows:
In the partition  , all partners value the
, all partners value the  -th piece as 1 and all other pieces as 0. Hence, in the matrix
-th piece as 1 and all other pieces as 0. Hence, in the matrix  , there are ones on the
, there are ones on the  -th column and zeros everywhere else.
-th column and zeros everywhere else.
By convexity, there is a partition  such that:
such that:
In that matrix, the  -th column contains only the value
-th column contains only the value  . This means that, in the partition
. This means that, in the partition  , all partners value the
, all partners value the  -th piece as exactly
-th piece as exactly  .
.
Note: this corollary confirms a previous assertion by Hugo Steinhaus. It also gives an affirmative answer to the problem of the Nile provided that there are only a finite number of flood heights.
Super-proportional division
A cake partition  to n pieces (one piece per partner) is called a super-proportional division with weights
to n pieces (one piece per partner) is called a super-proportional division with weights  if:
if:
I.e, the piece allotted to partner  is strictly more valuable for him than what he deserves. The following statement is Dubins-Spanier Theorem on the existence of super-proportional division {{rp|6}}
is strictly more valuable for him than what he deserves. The following statement is Dubins-Spanier Theorem on the existence of super-proportional division {{rp|6}}
|With these notations, let
 be weights whose sum is 1, assume that the point
be weights whose sum is 1, assume that the point  is an interior point of the (n-1)-dimensional simplex with coordinates pairwise different, and assume that the value measures
is an interior point of the (n-1)-dimensional simplex with coordinates pairwise different, and assume that the value measures 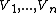 are normalized such that each partner values the entire cake as exactly 1 (i.e. they are non-atomic probability measures). If at least two of the measures
are normalized such that each partner values the entire cake as exactly 1 (i.e. they are non-atomic probability measures). If at least two of the measures 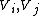 are not equal (
are not equal (  ), then super-proportional divisions exist.}}
), then super-proportional divisions exist.}}The hypothesis that the value measures 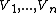 are not identical is necessary. Otherwise, the sum
are not identical is necessary. Otherwise, the sum  leads to a contradiction.
leads to a contradiction.
Namely, if all value measures are countably-additive and non-atomic, and if there are two partners  such that
such that  ,
,
then a super-proportional division exists.I.e, the necessary condition is also sufficient.
Sketch of Proof
Suppose w.l.o.g. that  . Then there is some piece of the cake,
. Then there is some piece of the cake, 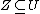 , such that
, such that  . Let
. Let 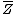 be the complement of
be the complement of  ; then
; then  . This means that
. This means that 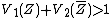 . However,
. However,  . Hence, either
. Hence, either 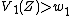 or
or  . Suppose w.l.o.g. that
. Suppose w.l.o.g. that  and
and 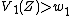 are true.
are true.
Define the following partitions:
-
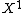 : the partition that gives
: the partition that gives  to partner 1,
to partner 1, 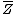 to partner 2, and nothing to all others.
to partner 2, and nothing to all others. -
 (for
(for  ): the partition that gives the entire cake to partner
): the partition that gives the entire cake to partner  and nothing to all others.
and nothing to all others.
Here, we are interested only in the diagonals of the matrices  , which represent the valuations of the partners to their own pieces:
, which represent the valuations of the partners to their own pieces:
- In
 , entry 1 is
, entry 1 is  , entry 2 is
, entry 2 is  , and the other entries are 0.
, and the other entries are 0. - In
 (for
(for  ), entry
), entry  is 1 and the other entires are 0.
is 1 and the other entires are 0.
By convexity, for every set of weights 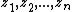 there is a partition
there is a partition  such that:
such that:
It is possible to select the weights  such that, in the diagonal of
such that, in the diagonal of  , the entries are in the same ratios as the weights
, the entries are in the same ratios as the weights  . Since we assumed that
. Since we assumed that 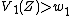 , it is possible to prove that
, it is possible to prove that  , so
, so  is a super-proportional division.
is a super-proportional division.
Utilitarian-optimal division
A cake partition  to n pieces (one piece per partner) is called utilitarian-optimal if it maximizes the sum of values. I.e, it maximizes:
to n pieces (one piece per partner) is called utilitarian-optimal if it maximizes the sum of values. I.e, it maximizes:
Utilitarian-optimal divisions do not always exist. For example, suppose  is the set of positive integers. There are two partners. Both value the entire set
is the set of positive integers. There are two partners. Both value the entire set  as 1. Partner 1 assigns a positive value to every integer and partner 2 assigns zero value to every finite subset. From a utilitarian point of view, it is best to give partner 1 a large finite subset and give the remainder to partner 2. When the set given to partner 1 becomes larger and larger, the sum-of-values becomes closer and closer to 2, but it never approaches 2. So there is no utilitarian-optimal division.
as 1. Partner 1 assigns a positive value to every integer and partner 2 assigns zero value to every finite subset. From a utilitarian point of view, it is best to give partner 1 a large finite subset and give the remainder to partner 2. When the set given to partner 1 becomes larger and larger, the sum-of-values becomes closer and closer to 2, but it never approaches 2. So there is no utilitarian-optimal division.
The problem with the above example is that the value measure of partner 2 is finitely-additive but not countably-additive.
The compactness part of the DS theorem immediately implies that:[1]{{rp|7}}
If all value measures are countably-additive and nonatomic,
then a utilitarian-optimal division exists.
In this special case, non-atomicity is not required: if all value measures are countably-additive, then a utilitarian-optimal partition exists.[1]{{rp|7}}
Leximin-optimal division
A cake partition  to n pieces (one piece per partner) is called leximin-optimal with weights
to n pieces (one piece per partner) is called leximin-optimal with weights  if it maximizes the lexicographically-ordered vector of relative values. I.e, it maximizes the following vector:
if it maximizes the lexicographically-ordered vector of relative values. I.e, it maximizes the following vector:
where the partners are indexed such that:
A leximin-optimal partition maximizes the value of the poorest partner (relative to his weight); subject to that, it maximizes the value of the next-poorest partner (relative to his weight); etc.
The compactness part of the DS theorem immediately implies that:[1]{{rp|8}}
If all value measures are countably-additive and nonatomic,
then a leximin-optimal division exists.
Further developments
- The leximin-optimality criterion, introduced by Dubins and Spanier, has been studied extensively later. In particular, in the problem of cake-cutting, it was studied by Marco Dall'Aglio.[3]
See also
- Lyapunov vector-measure theorem[4]
- Weller's theorem
References
2. ^{{Cite journal|doi=10.2140/pjm.1951.1.59|title=Relations among certain ranges of vector measures|journal=Pacific Journal of Mathematics|volume=1|pages=59|year=1951|last1=Dvoretzky|first1=A.|last2=Wald|first2=A.|last3=Wolfowitz|first3=J.}}
3. ^{{Cite journal|doi=10.1016/S0377-0427(99)00393-3|title=The Dubins–Spanier optimization problem in fair division theory|journal=Journal of Computational and Applied Mathematics|volume=130|pages=17|year=2001|last1=Dall'Aglio|first1=Marco}}
4. ^{{cite journal|last1=Neyman|first1=J|title=Un théorèm dʼexistence|journal=C. R. Acad. Sci.|date=1946|volume=222|pages=843–845}}
- Damien (play)
- Damien Pottinger
- Damien Ricketson
- Damien Robinson
- Damien Robitaille
- Damien Ryan
- Damien Saez
- Damien Sargue
- Damien Sin
- Damien smith
- Damien Smith
- Damien Smith (artist)
- Damien Smith (journalist)
- Damien Stone
- Damien Sully
- Damien The Leper Society
- Damien Thomas
- Damien Thorn
- Damien Tixier
- Damien Top
- Damien Traille
- Damien Trotter
- Damien Wayans
- Damien Wayne
- Damien Wayne Echols