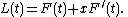“Pursuit curve”的意思、由来-开放百科全书

词条

Pursuit curve

释义

Single pursuer
Multiple pursuers
See also
External links

A curve of pursuit is a curve constructed by analogy to having a point or points representing pursuers and pursuees; the curve of pursuit is the curve traced by the pursuers.

With the paths of the pursuer and pursuee parameterized in time, the pursuee is always on the pursuer's tangent. That is, given {{math|F(t)}}, the pursuer (follower), and {{math|L(t)}}, the pursued (leader), for every {{mvar|t}} with {{math|F′(t) ≠ 0}} there is an {{mvar|x}} such that

Single pursuer

The path followed by a single pursuer, following a pursuee that moves at constant speed on a line, is a radiodrome. It is a solution of the differential equation

{{math|1+y' ² {{=}} k² (a−x²) y" ²}}.{{-}}

Multiple pursuers

Typical drawings of curves of pursuit have each point acting as both pursuer and pursuee, inside a polygon, and having each pursuer pursue the adjacent point on the polygon. An example of this is the mice problem.

External links

Mathworld, with a slightly narrower definition that |L′(t)| and |F′(t)| are constant
MacTutor Pursuit curve

1 : Curves

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Single pursuer

Multiple pursuers

See also

External links