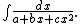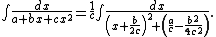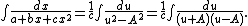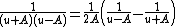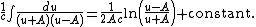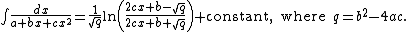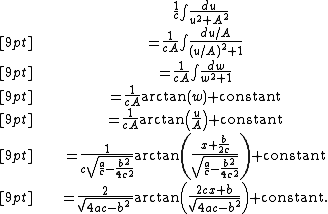“Quadratic integral”的意思、由来-开放百科全书

词条

Quadratic integral

释义

In mathematics, a quadratic integral is an integral of the form

It can be evaluated by completing the square in the denominator.

Positive-discriminant case

Assume that the discriminant q = b² − 4ac is positive. In that case, define u and A by

,

and

The quadratic integral can now be written as

The partial fraction decomposition

allows us to evaluate the integral:

The final result for the original integral, under the assumption that q > 0, is

This (hastily written) section may need attention.

In case the discriminant q = b² − 4ac is negative, the second term in the denominator in

is positive. Then the integral becomes

Weisstein, Eric W. "Quadratic Integral." From MathWorld--A Wolfram Web Resource, wherein the following is referenced:
{{cite book |author-first1=Izrail Solomonovich |author-last1=Gradshteyn |author-link1=Izrail Solomonovich Gradshteyn |author-first2=Iosif Moiseevich |author-last2=Ryzhik |author-link2=Iosif Moiseevich Ryzhik |author-first3=Yuri Veniaminovich |author-last3=Geronimus |author-link3=Yuri Veniaminovich Geronimus |author-first4=Michail Yulyevich |author-last4=Tseytlin |author-link4=Michail Yulyevich Tseytlin |author-first5=Alan |author-last5=Jeffrey |editor-first1=Daniel |editor-last1=Zwillinger |editor-first2=Victor Hugo |editor-last2=Moll |translator=Scripta Technica, Inc. |title=Table of Integrals, Series, and Products |publisher=Academic Press, Inc. |date=2015 |orig-year=October 2014 |edition=8 |language=English |isbn=0-12-384933-0 |id={{isbn|978-0-12-384933-5}} |lccn=2014010276 |title-link=Gradshteyn and Ryzhik}}

1 : Integral calculus

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。