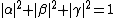“Qutrit”的意思、由来-开放百科全书

A qutrit (or quantum trit) is a unit of quantum information that is realized by a quantum system described by a superposition of three mutually orthogonal quantum states.^[1]

The qutrit is analogous to the classical base-3 trit, just as the qubit, a quantum system described by a superposition of two orthogonal states, is analogous to the classical base-2 bit.

Representation

A qutrit has three orthonormal basis states or vectors, often denoted

, and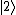

in Dirac or bra–ket notation.

These are used to describe the qutrit as a superposition state vector in the form of a linear combination of the three orthonormal basis states:

where the coefficients are complex probability amplitudes, such that the sum of their squares is unity (normalization):

The qubit's orthonormal basis states

span the two-dimensional complex Hilbert space

, corresponding to spin-up and spin-down of a spin-1/2 particle. Qutrits require a Hilbert space of higher dimension, namely the three-dimensional

spanned by the qutrit's basis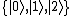

,^[2] which can be realized by a three-level quantum system. Note, however, that not all three-level quantum systems are qutrits.^[3]

A string of n qutrits represents 3ⁿ different states simultaneously, i.e., a superposition state vector in 3ⁿ-dimensional complex Hilbert space.^[4]

Qutrits have several peculiar features when used for storing quantum information. For example, they are more robust to decoherence under certain environmental interactions.^[5] In reality, manipulating qutrits directly might be tricky, and one way to do that is by using an entanglement with a qubit.^[6]

See also

References

1. ^{{Cite journal|last=Nisbet-Jones|first=Peter B. R.|last2=Dilley|first2=Jerome|last3=Holleczek|first3=Annemarie|last4=Barter|first4=Oliver|last5=Kuhn|first5=Axel|date=2013|title=Photonic qubits, qutrits and ququads accurately prepared and delivered on demand|url=http://stacks.iop.org/1367-2630/15/i=5/a=053007|journal=New Journal of Physics|language=en|volume=15|issue=5|pages=053007|doi=10.1088/1367-2630/15/5/053007|issn=1367-2630|arxiv=1203.5614}}
2. ^{{Cite journal|last=Byrd|first=Mark|date=1998|title=Differential geometry on SU(3) with applications to three state systems|url=http://aip.scitation.org/doi/10.1063/1.532618|journal=Journal of Mathematical Physics|language=en|volume=39|issue=11|pages=6125–6136|doi=10.1063/1.532618|issn=0022-2488|via=|arxiv=math-ph/9807032}}
3. ^{{Cite web|url=https://physics.stackexchange.com/questions/342903/quantum-systems-three-level-vs-qutrit|title=Quantum systems: three-level vs qutrit|website=Physics Stack Exchange|access-date=2018-07-25}}
4. ^{{Cite journal|last=Caves|first=Carlton M.|last2=Milburn|first2=Gerard J.|date=2000|title=Qutrit entanglement|url=https://doi.org/10.1016/S0030-4018(99)00693-8|journal=Optics Communications|volume=179|issue=1-6|pages=439–446|doi=10.1016/s0030-4018(99)00693-8|issn=0030-4018|via=}}
5. ^A. Melikidze, V. V. Dobrovitski, H. A. De Raedt, M. I. Katsnelson, and B. N. Harmon, Parity effects in spin decoherence, Phys. Rev. B 70, 014435 (2004) (link)
6. ^B. P. Lanyon,1 T. J. Weinhold, N. K. Langford, J. L. O'Brien, K. J. Resch, A. Gilchrist, and A. G. White, Manipulating Biphotonic Qutrits, Phys. Rev. Lett. 100, 060504 (2008) (link)

Representation

See also

References

External links