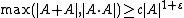- External links
- References
In arithmetic combinatorics, the Erdős–Szemerédi theorem, proven by Paul Erdős and Endre Szemerédi in 1983,[1] states that, for every finite set of real numbers, either the pairwise sums or the pairwise products of the numbers in the set form a significantly larger set. More precisely, it asserts the existence of positive constants c and 
such that
whenever A is a finite non-empty set of real numbers of cardinality |A|, where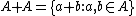 
is the sum-set of A with itself, and 
.
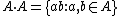It is possible for A + A to be of comparable size to A if A is an arithmetic progression, and it is possible for A · A to be of comparable size to A if A is a geometric progression. The Erdős–Szemerédi theorem can thus be viewed as an assertion that it is not possible for a large set to behave like an arithmetic progression and as a geometric progression simultaneously. It can also be viewed as an assertion that the real line does not contain any set resembling a finite subring or finite subfield; it is the first example of what is now known as the sum-product phenomenon, which is now known to hold in a wide variety of rings and fields, including finite fields.[2]
It was conjectured by Erdős and Szemerédi that one can take arbitrarily close to 1. The best result in this direction currently is by George Shakan,[3] who showed that one can take arbitrarily close to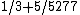 
. Previously, Misha Rudnev, Ilya Shkredov, and Sophie Stevens had shown that one can take arbitrarily close to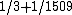 
,[4] improving an earlier result by József Solymosi,[5] who had shown that one can take it arbitrarily close to 
.
External links
- [https://www.quantamagazine.org/the-sum-product-problem-shows-how-addition-and-multiplication-constrain-each-other-20190206/ How a Strange Grid Reveals Hidden Connections Between Simple Numbers] - Quanta Magazine article about the sum-product phenomenon.
References
2. ^{{citation | last = Tao | first = Terence | author-link = Terence Tao | arxiv = 0806.2497 | issue = 2 | journal = Contributions to Discrete Mathematics | mr = 2592424 | pages = 59–82 | title = The sum-product phenomenon in arbitrary rings | volume = 4 | hdl=10515/sy5r78637 | year = 2009| bibcode = 2008arXiv0806.2497T }}.
3. ^{{cite arxiv|last=Shakan|first=George|date=2018|title=On higher energy decompositions and the sum-product phenomenon|eprint=1803.04637|class=math.NT}}
4. ^{{cite arxiv|last=Rudnev|first=Misha|last2=Shkredov|first2=Ilya D.|last3=Stevens|first3=Sophie|date=2016|title=On The Energy Variant of the Sum-Product Conjecture|eprint=1607.05053|class=math.CO}}
5. ^{{citation | last = Solymosi | first = József | authorlink = József Solymosi | arxiv = 0806.1040 | doi = 10.1016/j.aim.2009.04.006 | issue = 2 | journal = Advances in Mathematics | mr = 2538014 | pages = 402–408 | title = Bounding multiplicative energy by the sumset | volume = 222 | year = 2009}}.
- History of Las Animas, Colorado
- History of La Sarraz
- History of Las Cruces, New Mexico
- History of La Serena, Chile
- History of Lashkar Gah
- History of Las Khorey
- History of Las Margaritas, Chiapas
- History of Las Palmas
- History of Las Piedras, Uruguay
- History of Las Piñas
- History of Lassen County, California
- History of Lastrup, Minnesota
- History of Las Tunas (city)
- History of Las Vegas, New Mexico
- History of Latah County, Idaho
- History of Latakia
- History of late ancient Christianity
- History of Later Han
- History of Latexo, Texas
- History of Latham, Alabama
- History of Latham, Kansas
- History of Lathrop, California
- History of Lathrop, Missouri
- History of Lathrup Village, Michigan
- History of Latimer, Iowa