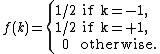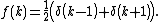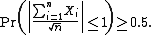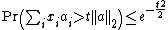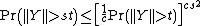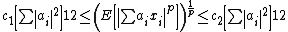请输入您要查询的百科知识：

　

词条 Rademacher distribution
释义

  1. Mathematical formulation

  2. Van Zuijlen's bound

  3. Bounds on sums

  4. Applications

  5. Related distributions

  6. References

{{Probability distribution|
  name       =Rademacher|  type       =mass|  pdf_image  =|  cdf_image  =|  parameters =|  support    =|  pdf        =|  cdf        =|  mean       =|  median     =|  mode       =N/A|  variance   =|  skewness   =|  kurtosis   =|  entropy    =|  mgf        =|  char       =|

}}

In probability theory and statistics, the Rademacher distribution (which is named after Hans Rademacher) is a discrete probability distribution where a random variate X has a 50% chance of being +1 and a 50% chance of being -1.[1]

A series of Rademacher distributed variables can be regarded as a simple symmetrical random walk where the step size is 1.

Mathematical formulation

The probability mass function of this distribution is

In terms of the Dirac delta function, as

Van Zuijlen's bound

Van Zuijlen has proved the following result.[2]

Let Xi be a set of independent Rademacher distributed random variables. Then

The bound is sharp and better than that which can be derived from the normal distribution (approximately Pr > 0.31).

Bounds on sums

Let {xi} be a set of random variables with a Rademacher distribution. Let {ai} be a sequence of real numbers. Then

where ||a||2 is the Euclidean norm of the sequence {ai}, t > 0 is a real number and Pr(Z) is the probability of event Z.[3]

Let Y = Σ xiai and let Y be an almost surely convergent series in a Banach space. The for t > 0 and s ≥ 1 we have[4]

for some constant c.

Let p be a positive real number. Then the Khintchine inequality says that[5]

where c1 and c2 are constants dependent only on p.

For p ≥ 1,

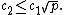
See also: Concentration inequality - a summary of tail-bounds on random variables.

Applications

The Rademacher distribution has been used in bootstrapping.

The Rademacher distribution can be used to show that normally distributed and uncorrelated does not imply independent.

Random vectors with components sampled independently from the Rademacher distribution are useful for various stochastic approximations, for example:

  • The Hutchinson trace estimator,[6] which can be used to efficiently approximate the trace of a matrix of which the elements are not directly accessible, but rather implicitly defined via matrix-vector products.
  • SPSA, a computationally cheap, derivative-free, stochastic gradient approximation, useful for numerical optimization.

Rademacher random variables are used in the Symmetrization Inequality.

Related distributions

  • Bernoulli distribution: If X has a Rademacher distribution, then 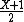has a Bernoulli(1/2) distribution.
  • Laplace distribution: If X has a Rademacher distribution and Y ~ Exp(λ), then XY ~ Laplace(0, 1/λ).

References

1. ^{{cite book |last=Hitczenko |first=P. |last2=Kwapień |first2=S. |year=1994 |chapter=On the Rademacher series |title=Probability in Banach Spaces |series=Progress in probability |volume=35 |pages=31–36 |doi=10.1007/978-1-4612-0253-0_2 |isbn=978-1-4612-6682-2 }}
2. ^{{cite journal |last=van Zuijlen |first=Martien C. A. |year=2011 |title=On a conjecture concerning the sum of independent Rademacher random variables |journal= |arxiv=1112.4988 |bibcode=2011arXiv1112.4988V }}
3. ^{{cite journal |last=Montgomery-Smith |first=S. J. |year=1990 |title=The distribution of Rademacher sums |journal=Proc Amer Math Soc |volume=109 |issue= 2|pages=517–522 |doi=10.1090/S0002-9939-1990-1013975-0 }}
4. ^{{cite journal |last=Dilworth |first=S. J. |last2=Montgomery-Smith |first2=S. J. |year=1993 |title=The distribution of vector-valued Radmacher series |journal=Ann Probab |volume=21 |issue=4 |pages=2046–2052 |jstor=2244710 |doi=10.1214/aop/1176989010 |arxiv=math/9206201 }}
5. ^{{cite journal |last=Khintchine |first=A. |year=1923 |title=Über dyadische Brüche |journal=Math. Z. |volume=18 |issue=1 |pages=109–116 |doi=10.1007/BF01192399 }}
6. ^{{cite journal |last=Avron |first=H. |last2=Toledo |first2=S. |title=Randomized algorithms for estimating the trace of an implicit symmetric positive semidefinite matrix |journal=Journal of the ACM |volume=58 |issue=2 |pages=8 |year=2011 |doi=10.1145/1944345.1944349 |citeseerx=10.1.1.380.9436 }}
{{ProbDistributions|discrete-finite}}{{DEFAULTSORT:Rademacher Distribution}}Distribuzione discreta uniforme#Altre distribuzioni

1 : Discrete distributions
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/14 22:45:30