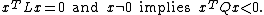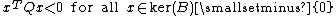- Statement of Finsler's lemma
- Variants
- Generalizations Projection lemma Robust version
- Applications S-Variable approach to robust control of linear dynamical systems Sufficient condition for universal stabilizability of non-linear systems
- See also
- References
Finsler's lemma is a mathematical result named after Paul Finsler. It states equivalent ways to express the positive definiteness of a quadratic form Q constrained by a linear form L.
Since it is equivalent to another lemmas used in optimization and control theory, such as Yakubovich's S-lemma[1], Finsler's lemma has been given many proofs and has been widely used, particularly in results related to robust optimization and linear matrix inequalities.
Statement of Finsler's lemma
Let {{math|x ∈ Rn}}, {{math|Q ∈ Rn x n}} and {{math|L ∈ Rn x n }} . The following statements are equivalent:[2]
Variants
In the particular case that L is positive semi-definite, it is possible to decompose it as {{math|1=L = BTB|L = }}. The following statements, which are also referred as Finsler's lemma in the literature, are equivalent:[3]
Generalizations
Projection lemma
The following statement, known as Projection Lemma (or also as Elimination Lemma), is common on the literature of linear matrix inequalities:[4]
This can be seen as a generalization of one of Finsler's lemma variants with the inclusion of an extra matrix and an extra constraint.
Robust version
Finsler's lemma also generalizes for matrices Q and B depending on a parameter s within a set S. In this case, it is natural to ask if the same variable μ (respectively X) can satisfy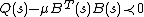 
for all 
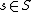(respectively, 
). If Q and B depends continuously on the parameter s, and S is compact, then this is true. If S is not compact, but Q and B are still continuous matrix-valued functions, then μ and X can be guaranteed to be at least continuous functions.[5]
Applications
S-Variable approach to robust control of linear dynamical systems
Finsler's lemma can be used to give novel linear matrix inequality (LMI) characterizations to stability and control problems.[3] The set of LMIs stemmed from this procedure yields less conservative results when applied to control problems where the system matrices has dependence on a parameter, such robust control problems and control of linear-parameter varying systems.[6] This approach has recently been called as S-variable approach[7][8] and the LMIs stemming from this approach are known as SV-LMIs (also known as dilated LMIs[9]).
Sufficient condition for universal stabilizability of non-linear systems
A non-linear system has the universal stabilizability property if every forward-complete solution of a system can be globally stabilized. By the use of Finsler's lemma, it is possible to derive a sufficient condition for universal stabilizability in terms of a differential linear matrix inequality.[10]
See also
- Linear matrix inequality
- S-lemma
- Elimination lemma
References
2. ^{{cite journal|last1=Finsler|first1=Paul|title=Über das Vorkommen definiter und semidefiniter Formen in Scharen quadratischer Formen|journal=Commentarii Mathematici Helvetici|volume=9|issue=1|pages=188–192|doi=10.1007/BF01258188|year=1936}}
3. ^1 {{cite book|title=Perspectives in robust control|last1=de Oliveira|first1=Maurício C.|last2=Skelton|first2=Robert E.|date=2001|publisher=Springer-Verlag|isbn=978-1-84628-576-9|editor1-last=Moheimani|editor1-first=S. O. Reza|location=London|pages=241–257|chapter=Stability tests for constrained linear systems}}
4. ^{{Cite book|title=Linear Matrix Inequalities in System and Control Theory|last=Boyd|first=S.|last2=El Ghaoui|first2=L.|last3=Feron|first3=E.|last4=Balakrishnan|first4=V.|date=1994-01-01|publisher=Society for Industrial and Applied Mathematics|isbn=9780898714852|series=Studies in Applied and Numerical Mathematics|doi=10.1137/1.9781611970777}}
5. ^{{Cite journal|last=Ishihara|first=J. Y.|last2=Kussaba|first2=H. T. M.|last3=Borges|first3=R. A.|date=August 2017|title=Existence of Continuous or Constant Finsler's Variables for Parameter-Dependent Systems|url=http://ieeexplore.ieee.org/document/7878619/|journal=IEEE Transactions on Automatic Control|volume=62|issue=8|pages=4187–4193|doi=10.1109/tac.2017.2682221|issn=0018-9286|arxiv=1711.04570}}
6. ^{{Cite journal|last=Oliveira|first=R. C. L. F.|last2=Peres|first2=P. L. D.|date=July 2007|title=Parameter-Dependent LMIs in Robust Analysis: Characterization of Homogeneous Polynomially Parameter-Dependent Solutions Via LMI Relaxations|url=http://ieeexplore.ieee.org/document/4268388/|journal=IEEE Transactions on Automatic Control|volume=52|issue=7|pages=1334–1340|doi=10.1109/tac.2007.900848|issn=0018-9286}}
7. ^{{Cite book|title=S-Variable Approach to LMI-Based Robust Control {{!}} SpringerLink|last=Ebihara|first=Yoshio|last2=Peaucelle|first2=Dimitri|last3=Arzelier|first3=Denis|language=en-gb|doi=10.1007/978-1-4471-6606-1|series = Communications and Control Engineering|year = 2015|isbn = 978-1-4471-6605-4}}
8. ^{{Cite book|last=Hosoe|first=Y.|last2=Peaucelle|first2=D.|date=June 2016|title=S-variable approach to robust stabilization state feedback synthesis for systems characterized by random polytopes|url=http://ieeexplore.ieee.org/document/7810589/|journal=2016 European Control Conference (ECC)|pages=2023–2028|doi=10.1109/ecc.2016.7810589|isbn=978-1-5090-2591-6}}
9. ^{{Cite book|last=Ebihara|first=Y.|last2=Hagiwara|first2=T.|date=August 2002|title=A dilated LMI approach to robust performance analysis of linear time-invariant uncertain systems|url=http://ieeexplore.ieee.org/document/1195827/|journal=Proceedings of the 41st SICE Annual Conference. SICE 2002.|volume=4|pages=2585–2590 vol.4|doi=10.1109/sice.2002.1195827|isbn=978-0-7803-7631-1}}
10. ^{{Cite journal|last=Manchester|first=I. R.|last2=Slotine|first2=J. J. E.|date=June 2017|title=Control Contraction Metrics: Convex and Intrinsic Criteria for Nonlinear Feedback Design|url=http://ieeexplore.ieee.org/document/7852456/|journal=IEEE Transactions on Automatic Control|volume=62|issue=6|pages=3046–3053|doi=10.1109/tac.2017.2668380|issn=0018-9286|arxiv=1503.03144}}