“Formally smooth map”的意思、由来-开放百科全书

词条

Formally smooth map

释义

References

In algebraic geometry and commutative algebra, a ring homomorphism is called formally smooth (from French: Formellement lisse) if it satisfies the following infinitesimal lifting property:

Suppose B is given the structure of an A-algebra via the map f. Given a commutative A-algebra, C, and a nilpotent ideal 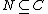, any A-algebra homomorphism may be lifted to an A-algebra map 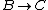. If moreover any such lifting is unique, then f is said to be formally étale.^[1]^[2]

Formally smooth maps were defined by Alexander Grothendieck in Éléments de géométrie algébrique IV.

For finitely presented morphisms, formal smoothness is equivalent to usual notion of smoothness.

References

1. ^{{EGA|book=4-1| pages = 5–259}}
2. ^{{EGA|book=4-4| pages = 5–361}}

2 : Commutative algebra|Algebraic geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。