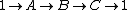“Formation (group theory)”的意思、由来-开放百科全书

词条

Formation (group theory)

释义

Special cases
Schunck classes
References

In mathematical group theory, a formation is a class of groups closed under taking images and such that if G/M and G/N are in the formation then so is G/M∩N. {{harvtxt|Gaschütz|1962}} introduced formations to unify the theory of Hall subgroups and Carter subgroups of finite solvable groups.

Some examples of formations are the formation of p-groups for a prime p, the formation of π-groups for a set of primes π, and the formation of nilpotent groups.

Special cases

A Melnikov formation is closed under taking quotients, normal subgroups and group extensions. Thus a Melnikov formation M has the property that for every short exact sequence

A and C are in M if and only if B is in M.^[1]

A full formation is a Melnikov formation which is also closed under taking subgroups.^[1]

An almost full formation is one which is closed under quotients, direct products and subgroups, but not necessarily extensions. The families of finite Abelian groups and finite nilpotent groups are almost full, but neither full nor Melnikov.^[2]

Schunck classes

A Schunck class, introduced by {{harvtxt|Schunck|1967}}, is a generalization of a formation, consisting of a class of groups such that a group is in the class if and only if every primitive factor group is in the class. Here a group is called primitive if it has a self-centralizing normal abelian subgroup.

References

1. ^¹Fried & Jarden (2004) p.344
2. ^Fried & Jarden (2004) p.542

{{Citation | last1=Ballester-Bolinches | first1=Adolfo | last2=Ezquerro | first2=Luis M. | title=Classes of finite groups | url=https://books.google.com/books?id=VoQ53SosWLIC | publisher=Springer-Verlag | location=Berlin, New York | series=Mathematics and Its Applications (Springer) | isbn=978-1-4020-4718-3 | mr=2241927 | year=2006 | volume=584}}
{{Citation | last1=Doerk | first1=Klaus | last2=Hawkes | first2=Trevor | title=Finite soluble groups | url=https://books.google.com/books?id=E7iL1eWB1TkC | publisher=Walter de Gruyter & Co. | location=Berlin | series=de Gruyter Expositions in Mathematics | isbn=978-3-11-012892-5 | mr=1169099 | year=1992 | volume=4}}
{{citation | last1=Fried | first1=Michael D. | last2=Jarden | first2=Moshe | title=Field arithmetic | edition=2nd revised and enlarged | series=Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge | volume=11 | publisher=Springer-Verlag | year=2004 | isbn=3-540-22811-X | zbl=1055.12003 }}
{{Citation | last1=Gaschütz | first1=Wolfgang | title=Zur Theorie der endlichen auflösbaren Gruppen | mr=0179257 | year=1962 | journal=Mathematische Zeitschrift | issn=0025-5874 | volume=80 | pages=300–305 | doi=10.1007/BF01162386}}
{{Citation | last1=Huppert | first1=Bertram | author1-link=Bertram Huppert | title=Endliche Gruppen | publisher=Springer-Verlag | location=Berlin, New York | language=German | isbn=978-3-540-03825-2 | oclc=527050 | mr=0224703 | year=1967}}
{{Citation | last1=Schunck | first1=Hermann | title=H-Untergruppen in endlichen auflösbaren Gruppen | doi=10.1007/BF01112173 | mr=0209356 | year=1967 | journal=Mathematische Zeitschrift | issn=0025-5874 | volume=97 | pages=326–330}}

1 : Group theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。