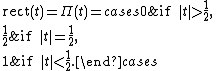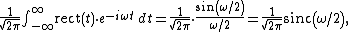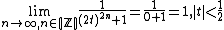“Rectangular function”的意思、由来-开放百科全书

词条

Rectangular function

释义

Relation to the boxcar function
Fourier transform of the rectangular function
Relation to the triangular function
Use in probability
Rational approximation
Demonstration of validity
See also
References

{{Use American English|date = March 2019}}{{Short description|Function whose graph is 0, then 1, then 0 again, in an almost-everywhere continuous way}}{{for|the periodic version|Rectangular wave}}

The rectangular function (also known as the rectangle function, rect function, Pi function, gate function, unit pulse, or the normalized boxcar function) is defined as^[1]

Alternative definitions of the function define to be 0,^[2] 1,^[3]^[4] or undefined.

Relation to the boxcar function

The rectangular function is a special case of the more general boxcar function:

where is the Heaviside function; the function is centered at and has duration , from to .

Fourier transform of the rectangular function

The unitary Fourier transforms of the rectangular function are^[1]

using ordinary frequency f, and

using angular frequency ω, where is the unnormalized form of the sinc function.

Note that as long as the definition of the pulse function is only motivated by its behavior in the time-domain experience, there is no reason to believe that the oscillatory interpretation (i.e. the Fourier transform function) should be intuitive, or directly understood by humans. However, some aspects of the theoretical result may be understood intuitively, as finiteness in time domain corresponds to an infinite frequency response. (Vice versa, a finite Fourier transform will correspond to infinite time domain response.)

Relation to the triangular function

We can define the triangular function as the convolution of two rectangular functions:

Use in probability

Viewing the rectangular function as a probability density function, it is a special case of the continuous uniform distribution with . The characteristic function is

and its moment-generating function is

where is the hyperbolic sine function.

Rational approximation

The pulse function may also be expressed as a limit of a rational function:

Demonstration of validity

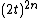First, we consider the case where . Notice that the term is always positive for integer . However, and hence 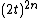approaches zero for large .

It follows that:

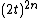Second, we consider the case where . Notice that the term is always positive for integer . However, 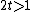and hence 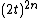grows very large for large .

It follows that:

Third, we consider the case where . We may simply substitute in our equation:

We see that it satisfies the definition of the pulse function.

References

1. ^¹{{MathWorld |title=Rectangle Function |id=RectangleFunction}}
2. ^{{Cite book |last=Wang |first=Ruye |title=Introduction to Orthogonal Transforms: With Applications in Data Processing and Analysis |page=135–136 |publisher=Cambridge University Press |year=2012 |url=https://books.google.com/books?id=4KEKGjaiJn0C&pg=PA135 |isbn=9780521516884 }}
3. ^{{Cite book |last=Tang |first=K. T. |title=Mathematical Methods for Engineers and Scientists: Fourier analysis, partial differential equations and variational models |page=85 |publisher=Springer |year=2007 |url=https://books.google.com/books?id=gG-ybR3uIGsC&pg=PA85 |isbn=9783540446958 }}
4. ^{{Cite book |last=Kumar |first=A. Anand |title=Signals and Systems |publisher=PHI Learning Pvt. Ltd. |page=258–260 |url=https://books.google.com/books?id=FGGa6BXhy3kC&pg=PA258 |isbn=9788120343108 |year=2011 }}

1 : Special functions

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。