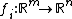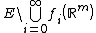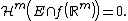“Rectifiable set”的意思、由来-开放百科全书

词条

Rectifiable set

释义

Definition
Rectifiable sets in metric spaces
Notes
References
External links

{{otheruses4|rectifiable sets in measure theory|rectifiable curves|Arc length}}

In mathematics, a rectifiable set is a set that is smooth in a certain measure-theoretic sense. It is an extension of the idea of a rectifiable curve to higher dimensions; loosely speaking, a rectifiable set is a rigorous formulation of a piece-wise smooth set. As such, it has many of the desirable properties of smooth manifolds, including tangent spaces that are defined almost everywhere. Rectifiable sets are the underlying object of study in geometric measure theory.

Definition

A subset of Euclidean space is said to be -rectifiable set if there exist a countable collection of continuously differentiable maps

such that the -Hausdorff measure 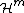of

is zero. The backslash here denotes the set difference. Equivalently, the may be taken to be Lipschitz continuous without altering the definition.^[1]

A set is said to be purely -unrectifiable if for every (continuous, differentiable) , one has

A standard example of a purely-1-unrectifiable set in two dimensions is the cross-product of the Smith–Volterra–Cantor set times itself.

Rectifiable sets in metric spaces

{{harvtxt|Federer|1969|pp=251–252}} gives the following terminology for m-rectifiable sets E in a general metric space X.

E is rectifiable when there exists a Lipschitz map 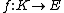for some bounded subset of onto .
E is countably rectifiable when E equals the union of a countable family of rectifiable sets.
E is countably 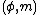rectifiable when is a measure on X and there is a countably rectifiable set F such that .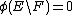
E is 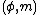rectifiable when E is countably 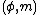rectifiable and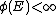
E is purely 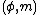unrectifiable when is a measure on X and E includes no rectifiable set F with .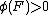

Definition 3 with 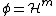and 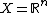comes closest to the above definition for subsets of Euclidean spaces.

Notes

1. ^{{harvnb|Simon|1984|p=58}}, calls this definition "countably m-rectifiable".

References

{{citation|ref=harv|last = Federer | first = Herbert | authorlink = Herbert Federer | title = Geometric measure theory| publisher = Springer-Verlag | location = New York | year = 1969 | pages = xiv+676 | isbn = 978-3-540-60656-7 | mr= 0257325 | series = Die Grundlehren der mathematischen Wissenschaften|volume=153}}
{{springer|author=T.C.O'Neil|id=G/g130040|title=Geometric measure theory}}
{{Citation|ref=harv

| last = Simon
| first = Leon
| author-link =Leon Simon
| title = Lectures on Geometric Measure Theory
| place = Canberra
| publisher = Centre for Mathematics and its Applications (CMA), Australian National University
| series = Proceedings of the Centre for Mathematical Analysis
| volume = 3
| year = 1984
| pages =VII+272 (loose errata)
| isbn = 0-86784-429-9
| zbl = 0546.49019
}}

External links

[https://www.encyclopediaofmath.org/index.php/Rectifiable_set Rectifiable set] at Encyclopedia of Mathematics

1 : Measure theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。