- History and background
- Calculation
- Applications
- References
In computational chemistry, the Fukui function or frontier function is a function that describes the electron density in a frontier orbital, as a result of a small change in the total number of electrons.[1]{{dead link|date=August 2017}} The condensed Fukui function or condensed reactivity indicator is the same idea, but applied to an atom within a molecule, rather than a point in three-dimensional space.
The Fukui function allows one to predict, using density functional theory, where the most electrophilic and nucleophilic sites of a molecule are.[2]
History and background
The Fukui function is named after Kenichi Fukui, who investigated the frontier orbitals described by the function, specifically the HOMO and LUMO.[3] Fukui functions are related in part to the frontier molecular orbital theory (also known as the Fukui theory of reactivity and selection, also developed by Kenichi Fukui) which discusses how nucleophiles attack the HOMO while at the same time placing their surplus electrons into the LUMO.[4]
Calculation
Most chemical reaction in general involves a change in electron density. The Fukui function indicates this change in electron density of a molecule at a given position when the number of electrons have been changed. The function itself can be quantified mathematically as follows:
 .
.
The Fukui function itself has two finite versions of this change which can be defined by the following two functions. The form of the function will depend on whether or not an electron was removed or added from the molecule. The Fukui function for the addition of an electron to a molecule is as follows:
 .
.
The next function will represent the Fukui function in terms of the removal of an electron from the molecule:
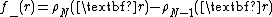 .
.
The  function represents the initial part of a nucleophilic reaction. The
function represents the initial part of a nucleophilic reaction. The  , on the other hand, represents the initial part of an electrophilic reaction. The reaction will therefore then take place where the
, on the other hand, represents the initial part of an electrophilic reaction. The reaction will therefore then take place where the  can be found to have a large value. Solving for either Fukui function would result in a representation of the molecule's electron density for either electrophilicity or nucleophilicity.[5]
can be found to have a large value. Solving for either Fukui function would result in a representation of the molecule's electron density for either electrophilicity or nucleophilicity.[5]
Applications
The Fukui function can be utilized in determining the reactivities of molecules towards other molecules. For example, the difference in the Fukui function before and after a CO molecule bonds with a nanoparticle surface can be used to interpret the nanoparticle's reactivity not only with CO but in other core-shell transition metal nanoparticles.[6]
The Fukui function has been shown to be related to the local softness of a system. This property has allowed it to be used for biological studies involving ligand docking, active site detection, and protein folding.[7]
References
2. ^{{cite book | isbn=9781420065435 | title = Chemical Reactivity Theory: A DFT View | year = 2010 | publisher = CRC Press | editor = Chatteraj, P. K. | author1 = Ayers, P. W. | author2 = Yang, W. | author3 = Bartolotti, L. J. | chapter = 18. Fukui Function | url = http://www.chem.duke.edu/~yang/people/65432_Book%20Chapter%2018FukuiFunction%20Ayers.pdf | format = reprint}}
3. ^Lewars, E.G. (2010). Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics. p.503. {{ISBN|9789048138623}}.
4. ^C. J. Cramer, Essentials of computational chemistry: theories and models, (Chichester, John Wiley, 2002)
5. ^F. Jensen, Introduction to Computational Chemistry, (Wiley, Chichester, 1999) p.492.
6. ^Allison, T.C., Tong, Y.J. (2012). Application of the condensed Fukui function to predict reactivity in core–shell transition metal nanoparticles. Electrochimica Acta, Volume 101, page 334-340.
7. ^Farver, J., Merz, K.M. (2010). The Utility of the HSAB Principle via the Fukui Function in Biological Systems. JCTC, vol. 6, p.548-559.
- Players Tour Championship 2010/2011 – Event 4
- Players Tour Championship 2010/2011 – Event 5
- Players Tour Championship 2010/2011 – Event 6
- Players Tour Championship 2010/2011 – Finals
- Players Union
- Players vs. angeles caidos
- Players who have converted from one football code to another
- Players Workshop
- Player Tour Championship
- Player Tour Championship 2010/2011
- Player Tour Championship 2010/2011 - Event 1
- Player Tour Championship 2010/2011 – Event 1
- Player Uno
- Player versus All
- Player versus Enviroment
- Player versus monsters
- Player-versus-player
- Player (video games)
- Player Violin
- Player vs All
- Player vs. All
- Player Vs. Player
- Play (ethology)
- Playfair Cipher
- Playfair (disambiguation)