- Definition
- Theorem for the relationship between fusion frames and global frames
- Local frame representation
- Definition of fusion frame operator
- Properties of fusion frame operator
- Representation of fusion frame operator
- References
- External links
- See also
In mathematics, a fusion frame of a vector space is a natural extension of a frame. It is an additive construct of several, potentially "overlapping" frames. The motivation for this concept comes from the event that a signal can not be acquired by a single sensor alone (a constraint found by limitations of hardware or data throughput), rather the partial components of the signal must be collected via a network of sensors, and the partial signal representations are then fused into the complete signal.
By construction, fusion frames easily lend themselves to parallel or distributed processing[1] of sensor networks consisting of arbitrary overlapping sensor fields.
Definition
Given a Hilbert space  , let
, let 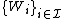 be closed subspaces of
be closed subspaces of  , where
, where  is an index set. Let
is an index set. Let 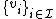 be a set of positive scalar weights. Then
be a set of positive scalar weights. Then 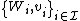 is a fusion frame of
is a fusion frame of  if there exist constants
if there exist constants 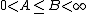 such that for all
such that for all 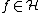 we have
we have
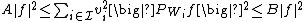 ,
,
where 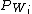 denotes the orthogonal projection onto the subspace
denotes the orthogonal projection onto the subspace  . The constants
. The constants  and
and  are called lower and upper bound, respectively. When the lower and upper bounds are equal to each other,
are called lower and upper bound, respectively. When the lower and upper bounds are equal to each other, 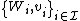 becomes a
becomes a  -tight fusion frame. Furthermore, if
-tight fusion frame. Furthermore, if 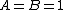 , we can call
, we can call 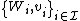 Parseval fusion frame.[1]
Parseval fusion frame.[1]
Assume 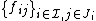 is a frame for
is a frame for  . Then
. Then  is called a fusion frame system for
is called a fusion frame system for  .[1]
.[1]
Theorem for the relationship between fusion frames and global frames
Let 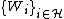 be closed subspaces of
be closed subspaces of  with positive weights
with positive weights 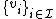 . Suppose
. Suppose 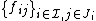 is a frame for
is a frame for  with frame bounds
with frame bounds 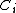 and
and  . Let
. Let 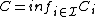 and
and 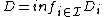 , which satisfy that
, which satisfy that  . Then
. Then 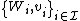 is a fusion frame of
is a fusion frame of  if and only if
if and only if  is a frame of
is a frame of  .
.
Additionally, if  is called a fusion frame system for
is called a fusion frame system for  with lower and upper bounds
with lower and upper bounds  and
and  , then
, then  is a frame of
is a frame of  with lower and upper bounds
with lower and upper bounds 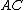 and
and 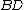 . And if
. And if  is a frame of
is a frame of  with lower and upper bounds
with lower and upper bounds  and
and  , then
, then  is called a fusion frame system for
is called a fusion frame system for  with lower and upper bounds
with lower and upper bounds 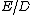 and
and 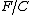 .[2]
.[2]
Local frame representation
Let 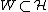 be a closed subspace, and let
be a closed subspace, and let 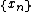 be an orthonormal basis of
be an orthonormal basis of  . Then for all
. Then for all 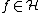 , the orthogonal projection of
, the orthogonal projection of  onto
onto  is given by
is given by  .[3]
.[3]
We can also express the orthogonal projection of  onto
onto  in terms of given local frame
in terms of given local frame  of
of  ,
,
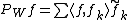 ,
,
where  is a dual frame of the local frame
is a dual frame of the local frame  .[1]
.[1]
Definition of fusion frame operator
Let 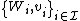 be a fusion frame for
be a fusion frame for  . Let
. Let 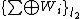 be representation space for projection. The analysis operator
be representation space for projection. The analysis operator  is defined by
is defined by
 .
.
Then The adjoint operator 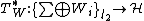 , which we call the synthesis operator, is given by
, which we call the synthesis operator, is given by
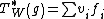 ,
,
where 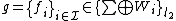 .
.
The fusion frame operator  is defined by
is defined by
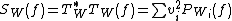 .[2]
.[2]Properties of fusion frame operator
Given the lower and upper bounds of the fusion frame 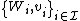 ,
,  and
and  , the fusion frame operator
, the fusion frame operator  can be bounded by
can be bounded by
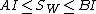 ,
,
where  is the identity operator. Therefore, the fusion frame operator
is the identity operator. Therefore, the fusion frame operator  is positive and invertible.[2]
is positive and invertible.[2]
Representation of fusion frame operator
Given a fusion frame system 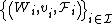 for
for  , where
, where  , and
, and 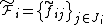 , which is a dual frame for
, which is a dual frame for 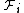 , the fusion frame operator
, the fusion frame operator  can be expressed as
can be expressed as
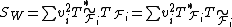 ,
,
where 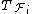 ,
, 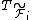 are analysis operators for
are analysis operators for 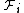 and
and 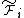 respectively, and
respectively, and  ,
, 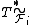 are synthesis operators for
are synthesis operators for 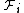 and
and 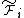 respectively.[1]
respectively.[1]
For finite frames (i.e., 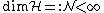 and
and 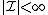 ), the fusion frame operator can be constructed with a matrix.[1] Let
), the fusion frame operator can be constructed with a matrix.[1] Let 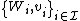 be a fusion frame for
be a fusion frame for  , and let
, and let 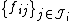 be a frame for the subspace
be a frame for the subspace  and
and 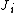 an index set for each
an index set for each 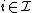 . With
. With
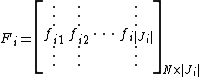
and
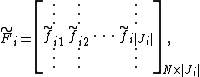
where  is the canonical dual frame of
is the canonical dual frame of  , the fusion frame operator
, the fusion frame operator 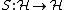 is given by
is given by
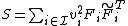 .
.
The fusion frame operator  is then given by an
is then given by an  matrix.
matrix.
References
2. ^1 2 {{cite book|last1=Casazza|first1=P.G.|last2=Kutyniok|first2=G.|title=Frames of subspaces|journal=Wavelets, Frames and Operator Theory|date=2004|volume=345|pages=87–113|doi=10.1090/conm/345/06242|series=Contemporary Mathematics|isbn=9780821833803}}
3. ^{{cite book|last=Christensen|first=Ole|title=An introduction to frames and Riesz bases|year=2003|publisher=Birkhäuser|location=Boston [u.a.]|isbn=978-0817642952|page=8}}
External links
- Fusion Frames
See also
- Hilbert space
- Frame (linear algebra)
- The Fan (Canadian radio network)
- The fancy
- The Fancy
- The Fancy Pants Adventures
- The Fang (frozen waterfall)
- The Fanjul Brothers
- The Fannie Farmer Cookbook
- The Fanny Farmer Cookbook
- The Fan, Richmond
- The Fan, Richmond, Virginia
- The Fantasist
- The Fantastic Adventures of Unico
- The Fantastic Flying Books of Mr Morris Lessmore
- The Fantastic Flying Books of Mr. Morris Lessmore
- The Fantastic Four 2
- The Fantastic Four (2015)
- The Fantastic Four (2015 film)
- The Fantastic Four (2015 reboot)
- The Fantastic Four 2 (2017 film)
- The Fantastic Four (film)
- The Fantastic Four (R&B group)
- The Fantastic Jazz Harp of Dorothy Ashby
- The Fantastic Johnny C
- The Fantastic Miss Piggy Show
- The Fantastic Voyages Of Sinbad The Sailor