“Remarkable cardinal”的意思、由来-开放百科全书

词条

Remarkable cardinal

释义

See also
References

In mathematics, a remarkable cardinal is a certain kind of large cardinal number.

A cardinal κ is called remarkable if for all regular cardinals θ > κ, there exist π, M, λ, σ, N and ρ such that

π : M → H_θ is an elementary embedding
M is countable and transitive
π(λ) = κ
σ : M → N is an elementary embedding with critical point λ
N is countable and transitive
ρ = M ∩ Ord is a regular cardinal in N
σ(λ) > ρ
M = H_ρ^N, i.e., M ∈ N and N ⊨ "M is the set of all sets that are hereditarily smaller than ρ"

Equivalently, is remarkable if and only if for every there is such that in some forcing extension 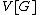, there is an elementary embedding satisfying . Note that, although the definition is similar to one of the definitions of supercompact cardinals, the elementary embedding here only has to exist in 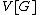, not in .

References

{{Citation | last1=Schindler | first1=Ralf | title=Proper forcing and remarkable cardinals | url=http://www.math.ucla.edu/~asl/bsl/0602/0602-003.ps | doi=10.2307/421205 | mr=1765054 | year=2000 | journal=The Bulletin of Symbolic Logic | issn=1079-8986 | volume=6 | issue=2 | pages=176–184| citeseerx=10.1.1.297.9314 }}
{{Citation | last1=Gitman | first1=Victoria | title=Virtual large cardinals | url=http://nylogic.org/wp-content/uploads/virtualLargeCardinals.pdf | year=2016 }}

1 : Large cardinals

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

See also

References