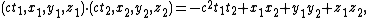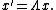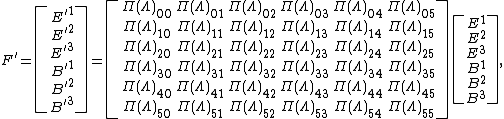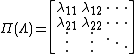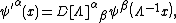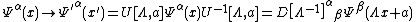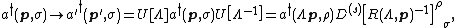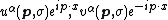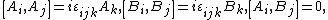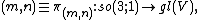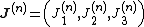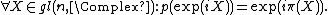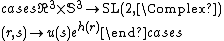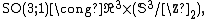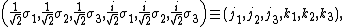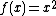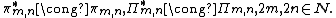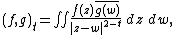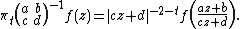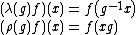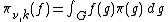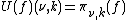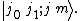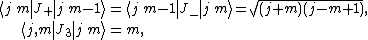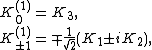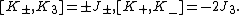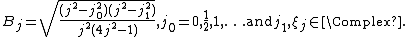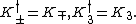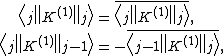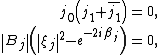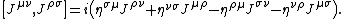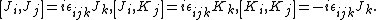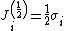- Non-technical introduction to representation theory Symmetry of space and time Lorentz transformations Multiplication table and representations Ordinary Lorentz transformations matrices do not suffice Finite-dimensional representations by matrices Infinite-dimensional representations by action on vector spaces of functions Infinite-dimensional representations viewed as infinite-dimensional matrices Lie algebra
- Applications Mathematics Classical field theory Relativistic quantum mechanics Quantum field theory Speculative theories
- Finite-dimensional representations History Technical introduction to finite-dimensional representation theory The Lie algebra The unitarian trick The representations The (μ, ν)-representations of sl(2, C) The (m, n)-representations of so(3; 1) Common representations The group Surjectiveness of exponential map for SO(3, 1) Fundamental group Projective representations The covering group SL(2, C) A geometric view An algebraic view Non-surjectiveness of exponential mapping for SL(2, C) Realization of representations of {{math|SL(2, C)}} and {{math|sl(2, C)}} and their Lie algebras Complex linear representations Real linear representations Properties of the (m, n) representations Dimension Faithfulness Non-unitarity Restriction to SO(3) Spinors Dual representations Complex conjugate representations The adjoint representation, the Clifford algebra, and the Dirac spinor representation The {{math|({{sfrac|1|2}}, 0) ⊕ (0, {{sfrac|1|2}})}} spin representation Reducible representations Space inversion and time reversal Space parity inversion Time reversal
- Action on function spaces Euclidean rotations The Möbius group The Riemann P-functions History Principal series for SL(2, C) Complementary series for SL(2, C) Plancherel theorem for SL(2, C) Classification of representations of SO(3, 1) Step 1 Step 2 Step 3 Step 4
- Explicit formulas Conventions and Lie algebra bases Weyl spinors and bispinors
- See also
- Remarks
- Notes
- Freely available online references
- References
The Lorentz group is a Lie group of symmetries of the spacetime of special relativity. This group can be realized as a collection of matrices, linear transformations, or unitary operators on some Hilbert space; it has a variety of representations. In any relativistically invariant physical theory, these representations must enter in some fashion;[1] physics itself must be made out of them. Indeed, special relativity together with quantum mechanics are the two physical theories that are most thoroughly established,[2] and the conjunction of these two theories is the study of the infinite-dimensional unitary representations of the Lorentz group. These have both historical importance in mainstream physics, as well as connections to more speculative present-day theories.
The full theory of the finite-dimensional representations of the Lie algebra of the Lorentz group is deduced using the general framework of the representation theory of semisimple Lie algebras. The finite-dimensional representations of the connected component  of the full Lorentz group {{math|O(3; 1)}} are obtained by employing the Lie correspondence and the matrix exponential. The full finite-dimensional representation theory of the universal covering group (and also the spin group, a double cover)
of the full Lorentz group {{math|O(3; 1)}} are obtained by employing the Lie correspondence and the matrix exponential. The full finite-dimensional representation theory of the universal covering group (and also the spin group, a double cover)  of
of  is obtained, and explicitly given in terms of action on a function space in representations of
is obtained, and explicitly given in terms of action on a function space in representations of  and
and  . The representatives of time reversal and space inversion are given in space inversion and time reversal, completing the finite-dimensional theory for the full Lorentz group. The general properties of the (m, n) representations are outlined. Action on function spaces is considered, with the action on spherical harmonics and the Riemann P-functions appearing as examples. The infinite-dimensional case of irreducible unitary representations are realized for the
. The representatives of time reversal and space inversion are given in space inversion and time reversal, completing the finite-dimensional theory for the full Lorentz group. The general properties of the (m, n) representations are outlined. Action on function spaces is considered, with the action on spherical harmonics and the Riemann P-functions appearing as examples. The infinite-dimensional case of irreducible unitary representations are realized for the  principal series and the complementary series. Finally, the Plancherel formula for
principal series and the complementary series. Finally, the Plancherel formula for  is given, and representations of {{math|SO(3, 1)}} are classified and realized for Lie algebras.
is given, and representations of {{math|SO(3, 1)}} are classified and realized for Lie algebras.
The development of the representation theory has historically followed the development of the more general theory of representation theory of semisimple groups, largely due to Élie Cartan and Hermann Weyl, but the Lorentz group has also received special attention due to its importance in physics. Notable contributors are physicist E. P. Wigner and mathematician Valentine Bargmann with their Bargmann–Wigner program,[3] one conclusion of which is, roughly, a classification of all unitary representations of the inhomogeneous Lorentz group amounts to a classification of all possible relativistic wave equations.[4] The classification of the irreducible infinite-dimensional representations of the Lorentz group was established by Paul Dirac's doctoral student in theoretical physics, Harish-Chandra, later turned mathematician,[5] in 1947. The corresponding classification for  was published independently by Bargmann and Israel Gelfand together with Mark Naimark in the same year.
was published independently by Bargmann and Israel Gelfand together with Mark Naimark in the same year.
The non-technical introduction contains some prerequisite material for readers not familiar with representation theory. Standard results used here from general finite-dimensional representation theory are outlined in technical introduction to finite-dimensional representation theory. The Lie algebra basis and other adopted conventions are given in conventions and Lie algebra bases. There is a substantially detailed article on the present subject to be found at Wikiversity.
Non-technical introduction to representation theory
The present purpose is to illustrate the role of representation theory of groups in mathematics and in physics. Rigor and detail take the back seat, as the main objective is to fix the notion of finite-dimensional and infinite-dimensional representations of the Lorentz group. The reader familiar with these concepts should skip by.
{{Hidden begin| titlestyle = color:green;background:lightgrey;|title=Prerequisites outlined}}Symmetry of space and time
{{Main|Symmetry (physics)#Spacetime symmetries|Spacetime symmetries|Lorentz group}}Space itself possesses symmetry. It looks the same no matter how one rotates it, and the resulting rotational symmetry is referred to as isotropy of space. In the present case it is common to use passive rotations, meaning that the observer[6] rotates themself. Mathematically, the active operation of a rotation is performed by multiplying position vectors by a rotation matrix. A passive rotation is accomplished by rotating only the basis vectors of the coordinate system. (The coordinate system can be thought of as being fixed in the rotated observer. The observer is physically rotated.) In this way, every point in space obtains new coordinates as if it was somehow physically rigidly rotated.
The Lorentz group contains all rotation matrices, extended to four dimensions with zeros in the first row and the first column except for the upper left element which is one, as elements.
There are, in addition, matrices that effect Lorentz boosts. These can be thought of, in the passive view, as (instantly!) giving the coordinate system (and with it the observer) a velocity in a chosen direction.
Finally, two special transformations are used to invert the coordinate system in space, space inversion, and in time, time reversal. In the first case, the space coordinate axes are reversed. The latter is reversal of the time direction. This is thought of, in the passive view, as having the observer set their clock at minus what it shows and then have the clock's hands move counterclockwise. Physical time progresses forward.
Mathematically the Lorentz group is defined as the set of transformations preserving the bilinear form
where the left-hand side is the Minkowski inner product of two events in spacetime, and the right-hand side is the spacetime interval, see classical group for mathematical detail.
Lorentz transformations
{{Main|Lorentz transformation}}In the spacetime of special relativity, called Minkowski space, space and time are interwoven. Thus the four coordinates of points in spacetime, called events, change in ways unexpected before the advent of special relativity, with time dilation and length contraction as two immediate consequences. The four-dimensional matrices of Lorentz transformations compose the Lorentz group. Its elements represent symmetries, and just like physical objects can be rotated using rotation matrices, the same physical objects (whose coordinates now include the time coordinate) can be transformed using the matrices representing Lorentz transformations. In particular, the four-vector representing an event in Lorentz frame transforms as
or on short form
Multiplication table and representations
{{Main|Cayley table|Representation theory}}The basic feature of every finite group is its multiplication table, also called Cayley table, that records the result of multiplying any two elements. A representation of a group can be thought of new set of elements, finite-dimensional or infinite-dimensional matrices, giving the same multiplication table after mapping the old elements to the new elements in a one-to-one fashion.[7] The same holds true in the case of an infinite group like the rotation group SO(3) or the Lorentz group. The multiplication table is just harder to visualize in the case of a group of uncountable size (same size as the set of reals). One way to do this is to wellorder the elements of the group with an ordinal number {{mvar|ρ}} being the order type. The "infinite Cayley table" is then indexed by two ordinals {{math|0 ≤ α, β ≤ ρ}} written in Cantor normal form.
Ordinary Lorentz transformations matrices do not suffice
The objects to be transformed may be something else than ordinary physical objects extending in three spatial dimensions (and time, unless the frame is the rest frame). It is for these objects that representation theory is needed for the mathematical description of transformations induced by ordinary Lorentz transformations of spacetime. For instance, the electromagnetic field is often (naively) envisaged by the assignment to each point in spacetime of a three-dimensional vector representing the electric field and another three-dimensional vector representing the magnetic field.
When space is rotated, the classically expected thing happens. The electric field and the magnetic field vectors at a designated point rotate with preserved length and angle between them.
Under Lorentz boosts they behave differently, showing that the two vectors aren't separate physical objects. The electric and magnetic components mix. See the illustration on the right. The electromagnetic field tensor displays the manifestly covariant mathematical structure of the electromagnetic field. It has six independent components at an event.[8]
Finite-dimensional representations by matrices
The problem of representation theory of the Lorentz group is, in the finite-dimensional case, to find new sets of matrices, not necessarily {{math|4 × 4}} in size that satisfies the same multiplication table as the matrices in the original Lorentz group. Returning to the example of the electromagnetic field, {{math|6 × 6}} matrices are needed that can be applied to a six-dimensional column vector containing the all together six components of the electromagnetic field. Thus {{math|6 × 6}}-matrices are sought for, such that
or in short
correctly expresses the transformation of the electromagnetic field under the Lorentz transformation {{math|Λ}}.[9] The same reasoning can be applied to Dirac's bispinors. While these have {{math|4}} components, the original {{math|4 × 4}}-matrices in the Lorentz group are inappropriate, even when restricted to rotations. Another {{math|4 × 4}}-representation is needed.
The sections dedicated to finite-dimensional representations are dedicated to exposing all such representations by finite-dimensional matrices that respect the multiplication table.
Infinite-dimensional representations by action on vector spaces of functions
Infinite-dimensional representations are usually realized as acting on sets of real or complex-valued functions on a set {{mvar|X}} endowed with a group action. A set being endowed with a group action {{mvar|A}} means, in essence, that if {{math|x ∈ X}} and {{math|g ∈ G}} that {{math|A(g)x {{=}} y}} with {{math|y ∈ X}}. If  denotes the set of all complex-valued functions on {{mvar|X}}, which is a vector space, a representation {{mvar|Π}} of {{mvar|G}} can be defined by[10]
denotes the set of all complex-valued functions on {{mvar|X}}, which is a vector space, a representation {{mvar|Π}} of {{mvar|G}} can be defined by[10]
The point to make is that again
and there is representation of {{mvar|G}}. This representation of {{mvar|G}} is finite-dimensional if and only if {{mvar|X}} is a finite set. This method is very general, and typically vector spaces of more specialized functions on sets close at hand are explored. Illustrating this procedure, a group {{mvar|G}} of {{math|n}}-dimensional matrices as a subset of Euclidean space 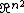 are considered, and the space of functions polynomials, perhaps of some maximum degree {{mvar|d}}, or even homogeneous polynomials of degree {{mvar|d}}, all defined on
are considered, and the space of functions polynomials, perhaps of some maximum degree {{mvar|d}}, or even homogeneous polynomials of degree {{mvar|d}}, all defined on  Those functions are then restricted to
Those functions are then restricted to  The set {{math|X {{=}} G}} automatically comes equipped with group actions, namely
The set {{math|X {{=}} G}} automatically comes equipped with group actions, namely
Here {{math|Lg}} denotes left action (by {{mvar|g}}), {{math|Rg}} denotes right action (by {{mvar|g}}), and {{math|Cg}} denotes conjugation (by {{mvar|g}}). With this sort of action, the vectors being acted on are functions. The resulting representations are (when the functions are unrestricted), in the first and second cases respectively, the left regular representation and the right regular representation of {{mvar|G}} on  [10]
[10]
The goal in the infinite-dimensional case of the representation theory is to classify all different possible representations, and to exhibit them in terms of vector spaces of functions and the action of the standard representation on the arguments of the functions.
Infinite-dimensional representations viewed as infinite-dimensional matrices
In order to relate representations on infinite-dimensional spaces to the finite-dimensional cases, an ordered basis is chosen for the vector space of functions and the action on basis functions under a given transformation is examined. Explicitly, if {{math|f1, f2, ...}} is a basis, compute
The coefficients of the basis functions in the expression for each transformed basis function is a column in the representative matrix. In general, the resulting matrix is countably infinite in dimension:[11]
Again, it is required that the set of infinite matrices obtained this way stand in one-to-one correspondence with the original {{math|4 × 4}}-matrices and that the multiplication table is the right one – the one of the {{math|4 × 4}}-matrices.[12] It should be emphasized that in the infinite-dimensional case, the concern is rarely the complete matrices. They are exposed here only to highlight the common thread. But individual matrix elements are frequently computed, especially for the Lie algebra (below).
Lie algebra
{{Main|Lie algebra}}The Lorentz group is a Lie group and has as such a Lie algebra, The Lie algebra is a vector space of matrices that can be said to model the group near the identity. It is endowed with a multiplication operation, the Lie bracket. With it, the product in the group can near the identity be expressed in Lie algebraic terms (but not in a particularly simple way). The link between the (matrix) Lie algebra and the (matrix) Lie group is the matrix exponential. It is one-to-one near the identity in the group.
Due to this it often suffices to find representations of the Lie algebra. Lie algebras are much simpler objects than Lie groups to work with. Due to the fact that the Lie algebra is a finite-dimensional vector space, in the case of the Lorentz Lie algebra the dimension is {{math|6}}, one need only find a finite number of representative matrices of the Lie algebra, one for each element of a basis of the Lie algebra as a vector space. The rest follow from extension by linearity, and the representation of the group is obtained by exponentiation.
One possible choice of basis for the Lie algebra is, in the standard representation, given in conventions and Lie algebra bases.
{{Hidden end}}Applications
Many of the representations, both finite-dimensional and infinite-dimensional, are important in theoretical physics. Representations appear in the description of fields in classical field theory, most importantly the electromagnetic field, and of particles in relativistic quantum mechanics, as well as of both particles and quantum fields in quantum field theory and of various objects in string theory and beyond. The representation theory also provides the theoretical ground for the concept of spin. The theory enters into general relativity in the sense that in small enough regions of spacetime, physics is that of special relativity.[13]
The finite-dimensional irreducible non-unitary representations together with the irreducible infinite-dimensional unitary representations of the inhomogeneous Lorentz group, the Poincare group, are the representations that have direct physical relevance.[14][15]
Infinite-dimensional unitary representations of the Lorentz group appear by restriction of the irreducible infinite-dimensional unitary representations of the Poincaré group acting on the Hilbert spaces of relativistic quantum mechanics and quantum field theory. But these are also of mathematical interest and of potential direct physical relevance in other roles than that of a mere restriction.[16] There were speculative theories,[17][19] (tensors and spinors have infinite counterparts in the expansors of Dirac and the expinors of Harish-Chandra) consistent with relativity and quantum mechanics, but they have found no proven physical application. Modern speculative theories potentially have similar ingredients per below.
Mathematics
From the point of view that the goal of mathematics is to classify and characterize, the representation theory of the Lorentz group is since 1947 a finished chapter. But in association with the Bargmann–Wigner programme, there are (as of 2006) yet unresolved purely mathematical problems, linked to the infinite-dimensional unitary representations.{{citation needed|date=September 2017}}
The irreducible infinite-dimensional unitary representations may have indirect relevance to physical reality in speculative modern theories since the (generalized) Lorentz group appears as the little group of the Poincaré group of spacelike vectors in higher spacetime dimension. The corresponding infinite-dimensional unitary representations of the (generalized) Poincaré group are the so-called tachyonic representations. Tachyons appear in the spectrum of bosonic strings and are associated with instability of the vacuum.[18][19] Even though tachyons may not be realized in nature, these representations must be mathematically understood in order to understand string theory. This is so since tachyon states turn out to appear in superstring theories too in attempts to create realistic models.[20]
One open problem (as of 2006) is the completion of the Bargmann–Wigner programme for the isometry group {{math|SO(D – 2, 1)}} of the de Sitter spacetime {{math|dSD – 2}}. Ideally, the physical components of wave functions would be realized on the hyperboloid {{math|dSD – 2}} of radius {{math|μ > 0}} embedded in  and the corresponding {{math|O(D − 2, 1)}} covariant wave equations of the infinite-dimensional unitary representation to be known.[19]
and the corresponding {{math|O(D − 2, 1)}} covariant wave equations of the infinite-dimensional unitary representation to be known.[19]
It is common in mathematics to regard the Lorentz group to be, foremost, the Möbius group to which it is isomorphic. The group may be represented in terms of a set of functions defined on the Riemann sphere. These are the Riemann P-functions, which are expressible as hypergeometric functions.{{citation needed|date=September 2017}}
Classical field theory
While the electromagnetic field together with the gravitational field are the only classical fields providing accurate descriptions of nature, other types of classical fields are important too. In the approach to quantum field theory (QFT) referred to as second quantization, the starting point is one or more classical fields, where e.g. the wave functions solving the Dirac equation are considered as classical fields prior to (second) quantization.[21] While second quantization and the Lagrangian formalism associated with it is not a fundamental aspect of QFT,[22] it is the case that so far all quantum field theories can be approached this way, including the standard model.[23] In these cases, there are classical versions of the field equations following from the Euler–Lagrange equations derived from the Lagrangian using the principle of least action. These field equations must be relativistically invariant, and their solutions (which will qualify as relativistic wave functions according to the definition below) must transform under some representation of the Lorentz group.
The action of the Lorentz group on the space of field configurations (a field configuration is the spacetime history of a particular solution, e.g. the electromagnetic field in all of space over all time is one field configuration) resembles the action on the Hilbert spaces of quantum mechanics, except that the commutator brackets are replaced by field theoretical Poisson brackets.[21]
Relativistic quantum mechanics
For the present purposes the following definition is made:[24] A relativistic wave function is a set of {{mvar|n}} functions {{math|ψα}} on spacetime which transforms under an arbitrary proper Lorentz transformation {{math|Λ}} as
where {{math|D[Λ]}} is an {{math|n}}-dimensional matrix representative of {{math|Λ}} belonging to some direct sum of the {{math|(m, n)}} representations to be introduced below.
The most useful relativistic quantum mechanics one-particle theories (there are no fully consistent such theories) are the Klein–Gordon equation[25] and the Dirac equation[26] in their original setting. They are relativistically invariant and their solutions transform under the Lorentz group as Lorentz scalars ({{math|(m, n) {{=}} (0, 0)}}) and bispinors respectively ({{math|(0, {{sfrac|1|2}}) ⊕ ({{sfrac|1|2}}, 0)}}). The electromagnetic field is a relativistic wave function according to this definition, transforming under {{math|(1, 0) ⊕ (0, 1)}}.[27]
The infinite-dimensional representations may be used in the analysis of scattering.[28]
Quantum field theory
In QFT, the demand for relativistic invariance enters, among other ways in that the S-matrix necessarily must be Poincaré invariant.[29] This has the implication that there is one or more infinite-dimensional representation of the Lorentz group acting on Fock space.[30] One way to guarantee the existence of such representations is the existence of a Lagrangian description (with modest requirements imposed, see the reference) of the system using the canonical formalism, from which a realization of the generators of the Lorentz group may be deduced.[31]
The transformations of field operators illustrate the complementary role played by the finite-dimensional representations of the Lorentz group and the infinite-dimensional unitary representations of the Poincare group, witnessing the deep unity between mathematics and physics.[32] For illustration, consider the definition an {{mvar|n}}-component field operator:[33] A relativistic field operator is a set of {{mvar|n}} operator valued functions on spacetime which transforms under proper Poincaré transformations {{math|(Λ, a)}} according to[34][35]
Here {{math|U[Λ, a]}} is the unitary operator representing {{math|(Λ, a)}} on the Hilbert space on which {{math|Ψ}} is defined and {{mvar|D}} is an {{mvar|n}}-dimensional representation of the Lorentz group. The transformation rule is the second Wightman axiom of quantum field theory.
By considerations of differential constraints that the field operator must be subjected to in order to describe a single particle with definite mass {{mvar|m}} and spin {{mvar|s}} (or helicity), it is deduced that[36][37]
{{NumBlk|:|
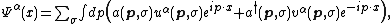
| {{EquationRef|X1|X1}}
}}
where {{math|a†, a}} are interpreted as creation and annihilation operators respectively. The creation operator {{math|a†}} transforms according to[36][38]
and similarly for the annihilation operator. The point to be made is that the field operator transforms according to a finite-dimensional non-unitary representation of the Lorentz group, while the creation operator transforms under the infinite-dimensional unitary representation of the Poincare group characterized by the mass and spin {{math|(m, s)}} of the particle. The connection between the two are the wave functions, also called coefficient functions
that carry both the indices {{math|(x, α)}} operated on by Lorentz transformations and the indices {{math|(p, σ)}} operated on by Poincaré transformations. This may be called the Lorentz–Poincaré connection.[39] To exhibit the connection, subject both sides of equation {{EquationNote|X1|(X1)}} to a Lorentz transformation resulting in for e.g. {{mvar|u}},
where {{mvar|D}} is the non-unitary Lorentz group representative of {{math|Λ}} and {{math|D(s)}} is a unitary representative of the so-called Wigner rotation {{mvar|R}} associated to {{math|Λ}} and {{math|p}} that derives from the representation of the Poincaré group, and {{mvar|s}} is the spin of the particle.
All of the above formulas, including the definition of the field operator in terms of creation and annihilation operators, as well as the differential equations satisfied by the field operator for a particle with specified mass, spin and the {{math|(m, n)}} representation under which it is supposed to transform,[40] and also that of the wave function, can be derived from group theoretical considerations alone once the frameworks of quantum mechanics and special relativity is given.[41]
Speculative theories
In theories in which spacetime can have more than {{math|D {{=}} 4}} dimensions, the generalized Lorentz groups {{math|O(D − 1; 1)}} of the appropriate dimension take the place of {{math|O(3; 1)}}.[42]
The requirement of Lorentz invariance takes on perhaps its most dramatic effect in string theory. Classical relativistic strings can be handled in the Lagrangian framework by using the Nambu–Goto action.[43] This results in a relativistically invariant theory in any spacetime dimension.[44] But as it turns out, the theory of open and closed bosonic strings (the simplest string theory) is impossible to quantize in such a way that the Lorentz group is represented on the space of states (a Hilbert space) unless the dimension of spacetime is 26.[45] The corresponding result for superstring theory is again deduced demanding Lorentz invariance, but now with supersymmetry. In these theories the Poincaré algebra is replaced by a supersymmetry algebra which is a {{math|Z2}}-graded Lie algebra extending the Poincaré algebra. The structure of such an algebra is to a large degree fixed by the demands of Lorentz invariance. In particular, the fermionic operators (grade {{math|1}}) belong to a {{math|(0, {{sfrac|1|2}})}} or {{math|({{sfrac|1|2}}, 0)}} representation space of the (ordinary) Lorentz Lie algebra.[46] The only possible dimension of spacetime in such theories is 10.[47]
Finite-dimensional representations
Representation theory of groups in general, and Lie groups in particular, is a very rich subject. The full Lorentz group is no exception. The Lorentz group has some properties that makes it "agreeable" and others that make it "not very agreeable" within the context of representation theory. The group is simple and thus semisimple, but is not connected, and none of its components are simply connected. Perhaps most importantly, the Lorentz group is not compact.[48]
For finite-dimensional representations, the presence of semisimplicity means that the Lorentz group can be dealt with the same way as other semisimple groups using a well-developed theory. In addition, all representations are built from the irreducible ones, since the Lie algebra possesses the complete reducibility property.[49][50] But, the non-compactness of the Lorentz group, in combination with lack of simple connectedness, cannot be dealt with in all the aspects as in the simple framework that applies to simply connected, compact groups. Non-compactness implies, for a connected simple Lie group, that no nontrivial finite-dimensional unitary representations exist.[51] Lack of simple connectedness gives rise to spin representations of the group.[52] The non-connectedness means that, for representations of the full Lorentz group, time reversal and space inversion has to be dealt with separately.[53][54]
History
The development of the finite-dimensional representation theory of the Lorentz group mostly follows that of the subject in general. Lie theory originated with Sophus Lie in 1873.[55][56] By 1888 the classification of simple Lie algebras was essentially completed by Wilhelm Killing.[57][58] In 1913 the theorem of highest weight for representations of simple Lie algebras, the path that will be followed here, was completed by Élie Cartan.[59][60] Richard Brauer was 1935–38 largely responsible for the development of the Weyl-Brauer matrices describing how spin representations of the Lorentz Lie algebra can be embedded in Clifford algebras.[61][62] The Lorentz group has also historically received special attention in representation theory, see History of infinite-dimensional unitary representations below, due to its exceptional importance in physics. Mathematicians Hermann Weyl[59][63][55][64][65] and Harish-Chandra[66][67] and physicists Eugene Wigner[68][69] and Valentine Bargmann[70][71][72] made substantial contributions both to general representation theory and in particular to the Lorentz group.[73] Physicist Paul Dirac was perhaps the first to manifestly knit everything together in a practical application of major lasting importance with the Dirac equation in 1928.[74][75][76]
Technical introduction to finite-dimensional representation theory
- For an overview of the strategy employed for the Lie algebra, overview of classification of Lie algebra representations is referred to.
- Techniques specific to noncompact groups can be found in unitarian trick and Lie algebra representations and Weyl's Unitarian trick.
- The passage from representations of a Lie algebra to the Lie group is covered in projective representations and matrix Lie group representations from Lie algebra representations.
The same material can be found, in more detailed form (in appropriate sequence and inline), in the Wikiversity version.
The Lie algebra
According to the strategy, the irreducible complex linear representations of the complexification, 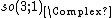 of the Lie algebra
of the Lie algebra  of the Lorentz group are to be found. A convenient basis for
of the Lorentz group are to be found. A convenient basis for  is given by the three generators {{math|Ji}} of rotations and the three generators {{math|Ki}} of boosts. They are explicitly given in conventions and Lie algebra bases.
is given by the three generators {{math|Ji}} of rotations and the three generators {{math|Ki}} of boosts. They are explicitly given in conventions and Lie algebra bases.
The Lie algebra is complexified, and the basis is changed to the components of its two ideals[77]
The components of {{math|A {{=}} (A1, A2, A3)}} and {{math|B {{=}} (B1, B2, B3)}} separately satisfy the commutation relations of the Lie algebra  and, moreover, they commute with each other,[78]
and, moreover, they commute with each other,[78]
where {{math|i, j, k}} are indices which each take values {{math|1, 2, 3}}, and {{math|εijk}} is the three-dimensional Levi-Civita symbol. Let  and
and 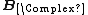 denote the complex linear span of {{math|A}} and {{math|B}} respectively.
denote the complex linear span of {{math|A}} and {{math|B}} respectively.
One has the isomorphisms[79][80]
{{Equation box 1| indent=
|equation = {{NumBlk|:
|
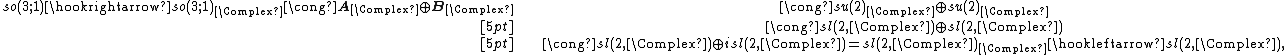
| {{EquationRef|A1|A1}}
| cellpadding=6
| border | border colour=#0073CF
| bgcolor=#F9FFF7
}}
where 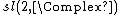 is the complexification of
is the complexification of 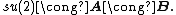
The utility of these isomorphisms comes from the fact that all irreducible representations of  , and hence (see strategy) all irreducible complex linear representations of
, and hence (see strategy) all irreducible complex linear representations of  are known. According to the final conclusion in strategy, the irreducible complex linear representation of
are known. According to the final conclusion in strategy, the irreducible complex linear representation of 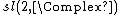 is isomorphic to one of the highest weight representations. These are explicitly given in complex linear representations of
is isomorphic to one of the highest weight representations. These are explicitly given in complex linear representations of 
The unitarian trick
The Lie algebra  is the Lie algebra of
is the Lie algebra of  It contains the compact subgroup {{math|SU(2) × SU(2)}} with Lie algebra
It contains the compact subgroup {{math|SU(2) × SU(2)}} with Lie algebra 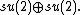 The latter is a compact real form of
The latter is a compact real form of 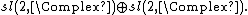 Thus from the first statement of the unitarian trick, representations of {{math|SU(2) × SU(2)}} are in one-to-one correspondence with holomorphic representations of
Thus from the first statement of the unitarian trick, representations of {{math|SU(2) × SU(2)}} are in one-to-one correspondence with holomorphic representations of 
By compactness, Peter–Weyl theorem applies to {{math|SU(2) × SU(2)}},[81] and hence orthonormality of irreducible characters may be appealed to. The irreducible unitary representations of {{math|SU(2) × SU(2)}} are precisely the tensor products of irreducible unitary representations of {{math|SU(2)}}.[82]
By appeal to simple connectedness, the second statement of the unitarian trick is applied. The objects in the following list are in one-to-one correspondence:
- Holomorphic representations of

- Smooth representations of {{math|SU(2) × SU(2)}}
- Real linear representations of

- Complex linear representations of

Tensor products of representations appear at the Lie algebra level as either of[83]
{{NumBlk|:|
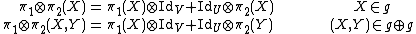
| {{EquationRef|A0|A0}}
}}
where {{math|Id}} is the identity operator. Here, the latter interpretation, which follows from {{EquationNote|G6|(G6)}}, is intended. The highest weight representations of 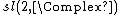 are indexed by {{mvar|μ}} for {{math|1=μ = 0, 1/2, 1, ...}}. (The highest weights are actually {{math|2μ {{=}} 0, 1, 2, ...}}, but the notation here is adapted to that of
are indexed by {{mvar|μ}} for {{math|1=μ = 0, 1/2, 1, ...}}. (The highest weights are actually {{math|2μ {{=}} 0, 1, 2, ...}}, but the notation here is adapted to that of  ) The tensor products of two such complex linear factors then form the irreducible complex linear representations of
) The tensor products of two such complex linear factors then form the irreducible complex linear representations of 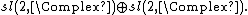
Finally, the 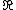 -linear representations of the real forms of the far left,
-linear representations of the real forms of the far left,  , and the far right,
, and the far right,  [84] in {{EquationNote|A1|(A1)}} are obtained from the
[84] in {{EquationNote|A1|(A1)}} are obtained from the  -linear representations of
-linear representations of  characterized in the previous paragraph.
characterized in the previous paragraph.
The representations
The real linear representations for 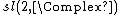 and
and  follow here assuming the complex linear representations of
follow here assuming the complex linear representations of 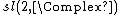 are known. Explicit realizations and group representations are given later.
are known. Explicit realizations and group representations are given later.
The (μ, ν)-representations of sl(2, C)
The complex linear representations of the complexification of 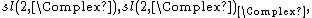 obtained via isomorphisms in {{EquationNote|A1|(A1)}}, stand in one-to-one correspondence with the real linear representations of
obtained via isomorphisms in {{EquationNote|A1|(A1)}}, stand in one-to-one correspondence with the real linear representations of  [85] The set of all, at least real linear, irreducible representations of
[85] The set of all, at least real linear, irreducible representations of 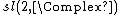 are thus indexed by a pair {{math|(μ, ν)}}. The complex linear ones, corresponding precisely to the complexification of the real linear
are thus indexed by a pair {{math|(μ, ν)}}. The complex linear ones, corresponding precisely to the complexification of the real linear  representations, are of the form {{math|(μ, 0)}}, while the conjugate linear ones are the {{math|(0, ν)}}.[85] All others are real linear only. The linearity properties follow from the canonical injection, the far right in {{EquationNote|A1|(A1)}}, of
representations, are of the form {{math|(μ, 0)}}, while the conjugate linear ones are the {{math|(0, ν)}}.[85] All others are real linear only. The linearity properties follow from the canonical injection, the far right in {{EquationNote|A1|(A1)}}, of 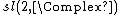 into its complexification. Representations on the form {{math|(ν, ν)}} or {{math|(μ, ν) ⊕ (ν, μ)}} are given by real matrices (the latter are not irreducible). Explicitly, the real linear {{math|(μ, ν)}}-representations of
into its complexification. Representations on the form {{math|(ν, ν)}} or {{math|(μ, ν) ⊕ (ν, μ)}} are given by real matrices (the latter are not irreducible). Explicitly, the real linear {{math|(μ, ν)}}-representations of 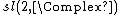 are
are
| indent=
| equation=
| cellpadding=6
| border | border colour=#0073CF
| bgcolor=#F9FFF7
}}
where  are the complex linear irreducible representations of
are the complex linear irreducible representations of 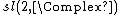 and
and 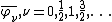 their complex conjugate representations. (The labeling is usually in the mathematics literature {{math|0, 1, 2, …}}, but half-integers are chosen here to conform with the labeling for the
their complex conjugate representations. (The labeling is usually in the mathematics literature {{math|0, 1, 2, …}}, but half-integers are chosen here to conform with the labeling for the  Lie algebra.) Here the tensor product is interpreted in the former sense of {{EquationNote|A0|(A0)}}. These representations are concretely realized below.
Lie algebra.) Here the tensor product is interpreted in the former sense of {{EquationNote|A0|(A0)}}. These representations are concretely realized below.
The (m, n)-representations of so(3; 1)
Via the displayed isomorphisms in {{EquationNote|A1|(A1)}} and knowledge of the complex linear irreducible representations of  upon solving for {{math|J}} and {{math|K}}, all irreducible representations of
upon solving for {{math|J}} and {{math|K}}, all irreducible representations of 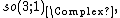 and, by restriction, those of
and, by restriction, those of  are obtained. The representations of
are obtained. The representations of  obtained this way are real linear (and not complex or conjugate linear) because the algebra is not closed upon conjugation, but they are still irreducible.[79] Since
obtained this way are real linear (and not complex or conjugate linear) because the algebra is not closed upon conjugation, but they are still irreducible.[79] Since  is semisimple,[79] all its representations can be built up as direct sums of the irreducible ones.
is semisimple,[79] all its representations can be built up as direct sums of the irreducible ones.
Thus the finite dimensional irreducible representations of the Lorentz algebra are classified by an ordered pair of half-integers {{math|1=m = μ}} and {{math|1=n = ν}}, conventionally written as one of
where {{mvar|V}} is a finite-dimensional vector space. These are, up to a similarity transformation, uniquely given by[86]
{{Equation box 1| indent=
| equation={{NumBlk|:
|

| {{EquationRef|A2|A2}}
| cellpadding=6
| border|border colour=#0073CF
| bgcolor=#F9FFF7
}}
where {{math|1n}} is the {{mvar|n}}-dimensional unit matrix and
are the {{math|(2n + 1)}}-dimensional irreducible representations of  also termed spin matrices or angular momentum matrices. These are explicitly given as[87]
also termed spin matrices or angular momentum matrices. These are explicitly given as[87]
where {{math|δ}} denotes the Kronecker delta. In components, with {{math|−m ≤ a, a′ ≤ m}}, {{math|−n ≤ b, b′ ≤ n}}, the representations are given by[88]
Common representations
| Scalar (1) | Left-handed Weyl spinor (2) | Self-dual 2-form (3) | (4) |
| Right-handed Weyl spinor (2) | 4-vector (4) | (6) | (8) |
| Anti-self-dual 2-form (3) | (6) | Traceless symmetric tensor (9) | (12) |
| (4) | (8) | (12) | (16) |
- The {{math|(0, 0)}} representation is the one-dimensional trivial representation and is carried by relativistic scalar field theories.
- Fermionic supersymmetry generators transform under one of the {{math|(0, {{sfrac|1|2}})}} or {{math|({{sfrac|1|2}}, 0)}} representations.[46]
- The four-momentum of a particle (either massless or massive) transforms under the {{math|({{sfrac|1|2}}, {{sfrac|1|2}})}} representation.
- A physical example of a traceless symmetric tensor field is the traceless[89] part of the energy-momentum tensor {{mvar|Tμν}}.[90][91]
Since for any irreducible representation for which {{math|m ≠ n}} it is essential to operate over the field of complex numbers, the direct sum of representations {{math|(m, n)}} and {{math|(n, m)}} have particular relevance to physics, since it permits to use linear operators over real numbers.
- {{math|({{sfrac|1|2}}, 0) ⊕ (0, {{sfrac|1|2}})}} is the bispinor representation. See also Dirac spinor and Weyl spinors and bispinors below.
- {{math|(1, {{sfrac|1|2}}) ⊕ ({{sfrac|1|2}}, 1)}} is the Rarita–Schwinger field representation.
- {{math|({{sfrac|3|2}}, 0) ⊕ (0, {{sfrac|3|2}})}} would be the symmetry of the hypothesized gravitino.[92] It can be obtained from the {{math|(1, {{sfrac|1|2}}) ⊕ ({{sfrac|1|2}}, 1)}} representation.[93]
- {{math|(1, 0) ⊕ (0, 1)}} is the representation of a parity-invariant 2-form field (a.k.a. curvature form). The electromagnetic field tensor transforms under this representation.
The group
The approach in this section is based on theorems that, in turn, are based on the fundamental Lie correspondence.[94] The Lie correspondence is in essence a dictionary between connected Lie groups and Lie algebras.[95] The link between them is the exponential mapping from the Lie algebra to the Lie group, denoted 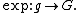 The general theory is summarized in technical introduction to finite-dimensional representation theory.
The general theory is summarized in technical introduction to finite-dimensional representation theory.
If 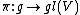 for some vector space {{mvar|V}} is a representation, a representation {{math|Π}} of the connected component of {{mvar|G}} is defined by
for some vector space {{mvar|V}} is a representation, a representation {{math|Π}} of the connected component of {{mvar|G}} is defined by
 |{{EquationRef|G2|G2}}}}
|{{EquationRef|G2|G2}}}}This definition applies whether the resulting representation is projective or not.
Surjectiveness of exponential map for SO(3, 1)
From a practical point of view, it is important whether the first formula in {{EquationNote|G2|(G2)}} can be used for all elements of the group. It holds for all 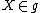 , however, in the general case, e.g. for
, however, in the general case, e.g. for  , not all {{math|g ∈ G}} are in the image of {{math|exp}}.
, not all {{math|g ∈ G}} are in the image of {{math|exp}}.
But 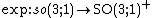 is surjective. One way to show this is to make use of the isomorphism
is surjective. One way to show this is to make use of the isomorphism  the latter being the Möbius group. It is a quotient of
the latter being the Möbius group. It is a quotient of 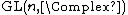 (see the linked article). The quotient map is denoted with
(see the linked article). The quotient map is denoted with  The map
The map  is onto.[96] Apply {{EquationNote|Lie|(Lie)}} with {{mvar|π}} being the differential of {{mvar|p}} at the identity. Then
is onto.[96] Apply {{EquationNote|Lie|(Lie)}} with {{mvar|π}} being the differential of {{mvar|p}} at the identity. Then
Since the left hand side is surjective (both {{math|exp}} and {{mvar|p}} are), the right hand side is surjective and hence  is surjective.[97] Finally, recycle the argument once more, but now with the known isomorphism between {{math|SO(3; 1)+}} and
is surjective.[97] Finally, recycle the argument once more, but now with the known isomorphism between {{math|SO(3; 1)+}} and  to find that {{math|exp}} is onto for the connected component of the Lorentz group.
to find that {{math|exp}} is onto for the connected component of the Lorentz group.
Fundamental group
The Lorentz group is doubly connected, i. e. {{math|π1(SO(3; 1))}} is a group with two equivalence classes of loops as its elements.
{{Hidden begin| titlestyle = color:green;background:lightgrey;|title=Proof}}To exhibit the fundamental group of {{math|SO(3; 1)+}}, the topology of its covering group  is considered. By the polar decomposition theorem, any matrix
is considered. By the polar decomposition theorem, any matrix  may be uniquely expressed as[98]
may be uniquely expressed as[98]
where {{mvar|u}} is unitary with determinant one, hence in {{math|SU(2)}}, and {{mvar|h}} is Hermitian with trace zero. The trace and determinant conditions imply:[99]
The manifestly continuous one-to-one map is a homeomorphism with continuous inverse given by (the locus of {{mvar|u}} is identified with  )
)
explicitly exhibiting that  is simply connected. But
is simply connected. But  where
where 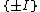 is the center of
is the center of  . Identifying {{mvar|λ}} and {{math|−λ}} amounts to identifying {{mvar|u}} with {{math|−u}}, which in turn amounts to identifying antipodal points on
. Identifying {{mvar|λ}} and {{math|−λ}} amounts to identifying {{mvar|u}} with {{math|−u}}, which in turn amounts to identifying antipodal points on  Thus topologically,[99]
Thus topologically,[99]
where last factor is not simply connected: Geometrically, it is seen (for visualization purposes,  may be replaced by
may be replaced by  ) that a path from {{mvar|u}} to {{math|−u}} in
) that a path from {{mvar|u}} to {{math|−u}} in  is a loop in
is a loop in  since {{mvar|u}} and {{math|−u}} are antipodal points, and that it is not contractible to a point. But a path from {{mvar|u}} to {{math|−u}}, thence to {{mvar|u}} again, a loop in
since {{mvar|u}} and {{math|−u}} are antipodal points, and that it is not contractible to a point. But a path from {{mvar|u}} to {{math|−u}}, thence to {{mvar|u}} again, a loop in  and a double loop (considering {{math|p(ueh) {{=}} p(−ueh)}}, where
and a double loop (considering {{math|p(ueh) {{=}} p(−ueh)}}, where  is the covering map) in
is the covering map) in  that is contractible to a point (continuously move away from {{math|−u}} "upstairs" in
that is contractible to a point (continuously move away from {{math|−u}} "upstairs" in  and shrink the path there to the point {{mvar|u}}).[99] Thus {{math|π1(SO(3; 1))}} is a group with two equivalence classes of loops as its elements, or put more simply, {{math|SO(3; 1)}} is doubly connected.
and shrink the path there to the point {{mvar|u}}).[99] Thus {{math|π1(SO(3; 1))}} is a group with two equivalence classes of loops as its elements, or put more simply, {{math|SO(3; 1)}} is doubly connected.
Projective representations
Since {{math|π1(SO(3; 1)+)}} has two elements, some representations of the Lie algebra will yield projective representations.[100][101] Once it is known whether a representation is projective, formula {{EquationNote|G2|(G2)}} applies to all group elements and all representations, including the projective ones — with the understanding that the representative of a group element will depend on which element in the Lie algebra (the {{mvar|X}} in {{EquationNote|G2|(G2)}}) is used to represent the group element in the standard representation.
For the Lorentz group, the {{math|(m, n)}}-representation is projective when {{math|m + n}} is a half-integer. See the section spinors.
For a projective representation {{math|Π}} of {{math|SO(3; 1)+}}, it holds that[99]
{{Equation box 1|indent=|equation={{NumBlk|:|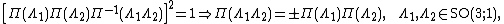 |{{EquationRef|G5|G5}}}}
|{{EquationRef|G5|G5}}}}|cellpadding=6|border|border colour=#0073CF|bgcolor=#F9FFF7}}
since any loop in {{math|SO(3; 1)+}} traversed twice, due to the double connectedness, is contractible to a point, so that its homotopy class is that of a constant map. It follows that {{math|Π}} is a double-valued function. It is not possible to consistently chose a sign to obtain a continuous representation of all of {{math|SO(3; 1)+}}, but this is possible locally around any point.[51]
The covering group SL(2, C)
Consider  as a real Lie algebra with basis
as a real Lie algebra with basis
where the sigmas are the Pauli matrices. From the relations
{{NumBlk|:| |{{EquationRef|J1|J1}}}}
|{{EquationRef|J1|J1}}}}is obtained
{{NumBlk|:| |{{EquationRef|J2|J2}}}}
|{{EquationRef|J2|J2}}}}which are exactly on the form of the {{math|3}}-dimensional version of the commutation relations for  (see conventions and Lie algebra bases below). Thus, the map {{math|Ji ↔ ji}}, {{math|Ki ↔ ki}}, extended by linearity is an isomorphism. Since
(see conventions and Lie algebra bases below). Thus, the map {{math|Ji ↔ ji}}, {{math|Ki ↔ ki}}, extended by linearity is an isomorphism. Since  is simply connected, it is the universal covering group of {{math|SO(3; 1)+}}.
is simply connected, it is the universal covering group of {{math|SO(3; 1)+}}.
 covering of the Lorentz group in particular}}
covering of the Lorentz group in particular}}A geometric view
Let {{math|pg(t), 0 ≤ t ≤ 1}} be a path from {{math|1 ∈ SO(3; 1)+}} to {{math|g ∈ SO(3; 1)+}}, denote its homotopy class by {{math|[pg]}} and let {{mvar|πg}} be the set of all such homotopy classes. Define the set
{{NumBlk|:| |{{EquationRef|C1|C1}}}}
|{{EquationRef|C1|C1}}}}and endow it with the multiplication operation
{{NumBlk|:| |{{EquationRef|C2|C2}}}}
|{{EquationRef|C2|C2}}}}where  is the path multiplication of
is the path multiplication of  and
and  :
:
With this multiplication, {{mvar|G}} becomes a group isomorphic to  [102] the universal covering group of {{math|SO(3; 1)+}}. Since each {{mvar|πg}} has two elements, by the above construction, there is a 2:1 covering map {{math|p : G → SO(3; 1)+}}. According to covering group theory, the Lie algebras
[102] the universal covering group of {{math|SO(3; 1)+}}. Since each {{mvar|πg}} has two elements, by the above construction, there is a 2:1 covering map {{math|p : G → SO(3; 1)+}}. According to covering group theory, the Lie algebras 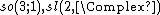 and
and  of {{mvar|G}} are all isomorphic. The covering map {{math|p : G → SO(3; 1)+}} is simply given by {{math|p(g, [pg]) {{=}} g}}.
of {{mvar|G}} are all isomorphic. The covering map {{math|p : G → SO(3; 1)+}} is simply given by {{math|p(g, [pg]) {{=}} g}}.
An algebraic view
For an algebraic view of the universal covering group, let  act on the set of all Hermitian {{gaps|2|×|2}} matrices
act on the set of all Hermitian {{gaps|2|×|2}} matrices  by the operation[99]
by the operation[99]
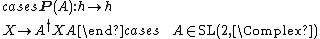 |{{EquationRef|C3|C3}}}}
|{{EquationRef|C3|C3}}}}The action on  is linear. An element of
is linear. An element of  may be written in the form
may be written in the form
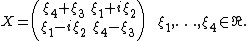 |{{EquationRef|C4|C4}}}}
|{{EquationRef|C4|C4}}}}The map {{math|P}} is a group homomorphism into  Thus
Thus 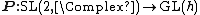 is a 4-dimensional representation of
is a 4-dimensional representation of  . Its kernel must in particular take the identity matrix to itself, {{math|A†IA {{=}} A†A {{=}} I}} and therefore {{math|A† {{=}} A−1}}. Thus {{math|AX {{=}} XA}} for {{mvar|A}} in the kernel so, by Schur's lemma,[103] {{mvar|A}} is a multiple of the identity, which must be {{math|±I}} since {{math|det A {{=}} 1}}.[104] The space
. Its kernel must in particular take the identity matrix to itself, {{math|A†IA {{=}} A†A {{=}} I}} and therefore {{math|A† {{=}} A−1}}. Thus {{math|AX {{=}} XA}} for {{mvar|A}} in the kernel so, by Schur's lemma,[103] {{mvar|A}} is a multiple of the identity, which must be {{math|±I}} since {{math|det A {{=}} 1}}.[104] The space  is mapped to Minkowski space {{math|M4}}, via
is mapped to Minkowski space {{math|M4}}, via
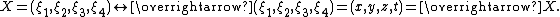 |{{EquationRef|C5|C5}}}}
|{{EquationRef|C5|C5}}}}The action of {{math|P(A)}} on  preserves determinants. The induced representation {{math|p}} of
preserves determinants. The induced representation {{math|p}} of  on
on  via the above isomorphism, given by
via the above isomorphism, given by
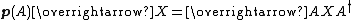 |{{EquationRef|C6|C6}}}}
|{{EquationRef|C6|C6}}}}preserves the Lorentz inner product since
This means that {{math|p(A)}} belongs to the full Lorentz group {{math|SO(3; 1)}}. By the main theorem of connectedness, since  is connected, its image under {{math|p}} in {{math|SO(3; 1)}} is connected, and hence is contained in {{math|SO(3; 1)+}}.
is connected, its image under {{math|p}} in {{math|SO(3; 1)}} is connected, and hence is contained in {{math|SO(3; 1)+}}.
It can be shown that the Lie map of 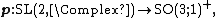 is a Lie algebra isomorphism:
is a Lie algebra isomorphism: 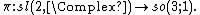 [105] The map {{math|P}} is also onto.[106]
[105] The map {{math|P}} is also onto.[106]
Thus  , since it is simply connected, is the universal covering group of {{math|SO(3; 1)+}}, isomorphic to the group {{mvar|G}} of above.
, since it is simply connected, is the universal covering group of {{math|SO(3; 1)+}}, isomorphic to the group {{mvar|G}} of above.
Non-surjectiveness of exponential mapping for SL(2, C)
The exponential mapping 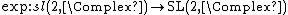 is not onto.[107] The matrix
is not onto.[107] The matrix
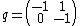 |{{EquationRef|S6|S6}}}}
|{{EquationRef|S6|S6}}}}is in  but there is no
but there is no 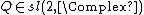 such that {{math|q {{=}} exp(Q)}}.[108]
such that {{math|q {{=}} exp(Q)}}.[108]
In general, if {{mvar|g}} is an element of a connected Lie group {{mvar|G}} with Lie algebra 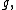 then, by {{EquationNote|Lie|(Lie)}},
then, by {{EquationNote|Lie|(Lie)}},
 |{{EquationRef|S7|S7}}}}
|{{EquationRef|S7|S7}}}}The matrix {{mvar|q}} can be written
{{NumBlk|:|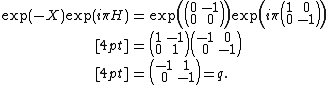 |{{EquationRef|S8|S8}}}}
|{{EquationRef|S8|S8}}}}Realization of representations of {{math|SL(2, C)}} and {{math|sl(2, C)}} and their Lie algebras
The complex linear representations of  and
and  are more straightforward to obtain than the
are more straightforward to obtain than the  representations. They can be (and usually are) written down from scratch. The holomorphic group representations (meaning the corresponding Lie algebra representation is complex linear) are related to the complex linear Lie algebra representations by exponentiation. The real linear representations of
representations. They can be (and usually are) written down from scratch. The holomorphic group representations (meaning the corresponding Lie algebra representation is complex linear) are related to the complex linear Lie algebra representations by exponentiation. The real linear representations of  are exactly the {{math|(μ, ν)}}-representations. They can be exponentiated too. The {{math|(μ, 0)}}-representations are complex linear and are (isomorphic to) the highest weight-representations. These are usually indexed with only one integer (but half-integers are used here).
are exactly the {{math|(μ, ν)}}-representations. They can be exponentiated too. The {{math|(μ, 0)}}-representations are complex linear and are (isomorphic to) the highest weight-representations. These are usually indexed with only one integer (but half-integers are used here).
The mathematics convention is used in this section for convenience. Lie algebra elements differ by a factor of {{math|i}} and there is no factor of {{math|i}} in the exponential mapping compared to the physics convention used elsewhere. Let the basis of  be[109]
be[109]
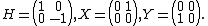 |{{EquationRef|S1|S1}}}}
|{{EquationRef|S1|S1}}}}This choice of basis, and the notation, is standard in the mathematical literature.
Complex linear representations
The irreducible holomorphic {{math|(n + 1)}}-dimensional representations 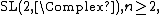 can be realized on the space of homogeneous polynomial of degree {{math|n}} in 2 variables
can be realized on the space of homogeneous polynomial of degree {{math|n}} in 2 variables 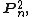 [110][111] the elements of which are
[110][111] the elements of which are
The action of  is given by[112][113]
is given by[112][113]
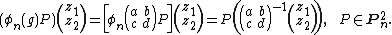 |{{EquationRef|S2|S2}}}}
|{{EquationRef|S2|S2}}}}The associated  -action is, using {{EquationNote|G6|(G6)}} and the definition above, for the basis elements of
-action is, using {{EquationNote|G6|(G6)}} and the definition above, for the basis elements of 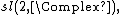 [114]
[114]
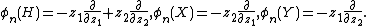 |{{EquationRef|S5|S5}}}}
|{{EquationRef|S5|S5}}}}With a choice of basis for  , these representations become matrix Lie algebras.
, these representations become matrix Lie algebras.
Real linear representations
The {{math|(μ, ν)}}-representations are realized on a space of polynomials  in
in  homogeneous of degree {{mvar|μ}} in
homogeneous of degree {{mvar|μ}} in 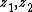 and homogeneous of degree {{mvar|ν}} in
and homogeneous of degree {{mvar|ν}} in  [111] The representations are given by[115]
[111] The representations are given by[115]
 |{{EquationRef|S6|S6}}}}|cellpadding=6|border|border colour=#0073CF|bgcolor=#F9FFF7}}
|{{EquationRef|S6|S6}}}}|cellpadding=6|border|border colour=#0073CF|bgcolor=#F9FFF7}}By employing {{EquationNote|G6|(G6)}} again it is found that
{{Equation box 1|indent=|equation={{NumBlk|:| |{{EquationRef|S7|S7}}}}
|{{EquationRef|S7|S7}}}}|cellpadding=6|border|border colour=#0073CF|bgcolor=#F9FFF7}}
In particular for the basis elements,:
{{Equation box 1|indent=|equation={{NumBlk|:| |{{EquationRef|S8|S8}}}}|cellpadding=6|border|border colour=#0073CF|bgcolor=#F9FFF7}}
|{{EquationRef|S8|S8}}}}|cellpadding=6|border|border colour=#0073CF|bgcolor=#F9FFF7}}Properties of the (m, n) representations
The {{math|(m, n)}} representations, defined above via {{EquationNote|A1|(A1)}} (as restrictions to the real form 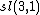 ) of tensor products of irreducible complex linear representations {{math|πm {{=}} μ}} and {{math|πn {{=}} ν}} of
) of tensor products of irreducible complex linear representations {{math|πm {{=}} μ}} and {{math|πn {{=}} ν}} of 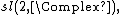 are irreducible, and they are the only irreducible representations.[116]
are irreducible, and they are the only irreducible representations.[116]
- Irreducibility follows from the unitarian trick[117] and that a representation {{math|Π}} of {{math|SU(2) × SU(2)}} is irreducible if and only if {{math|Π {{=}} Πμ ⊗ Πν}},[118] where {{math|Πμ, Πν}} are irreducible representations of {{math|SU(2)}}.
- Uniqueness follows from that the {{math|Πm}} are the only irreducible representations of {{math|SU(2)}}, which is one of the conclusions of the theorem of the highest weight.[119]
Dimension
The {{math|(m, n)}} representations are {{math|(2m + 1)(2n + 1)}}-dimensional.[120] This follows easiest from counting the dimensions in any concrete realization, such as the one given in representations of  and
and 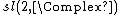 . For a Lie general algebra
. For a Lie general algebra  the Weyl dimension formula,[121]
the Weyl dimension formula,[121]
applies, where {{math|R+}} is the set of positive roots, {{math|ρ}} is the highest weight, and {{math|δ}} is half the sum of the positive roots. The inner product  is that of the Lie algebra
is that of the Lie algebra 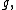 invariant under the action of the Weyl group on
invariant under the action of the Weyl group on 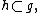 the Cartan subalgebra. The roots (really elements of
the Cartan subalgebra. The roots (really elements of 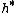 are via this inner product identified with elements of
are via this inner product identified with elements of  For
For 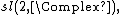 the formula reduces to {{math|dim πμ {{=}} 2μ + 1 {{=}} 2m + 1}}, where the present notation must be taken into account. The highest weight is {{math|2μ}}.[122] By taking tensor products, the result follows.
the formula reduces to {{math|dim πμ {{=}} 2μ + 1 {{=}} 2m + 1}}, where the present notation must be taken into account. The highest weight is {{math|2μ}}.[122] By taking tensor products, the result follows.
Faithfulness
If a representation {{math|Π}} of a Lie group {{math|G}} is not faithful, then {{math|N {{=}} ker Π}} is a nontrivial normal subgroup.[123] There are three relevant cases.
- {{math|N}} is non-discrete and abelian.
- {{math|N}} is non-discrete and non-abelian.
- {{math|N}} is discrete. In this case {{math|N ⊂ Z}}, where {{math|Z}} is the center of {{math|G}}.&91;124&93;
In the case of {{math|SO(3; 1)+}}, the first case is excluded since {{math|SO(3; 1)+}} is semi-simple.[125] The second case (and the first case) is excluded because {{math|SO(3; 1)+}} is simple.[126] For the third case, {{math|SO(3; 1)+}} is isomorphic to the quotient 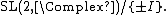 But
But 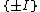 is the center of
is the center of 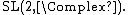 It follows that the center of {{math|SO(3; 1)+}} is trivial, and this excludes the third case. The conclusion is that every representation {{math|Π : SO(3; 1)+ → GL(V)}} and every projective representation {{math|Π : SO(3; 1)+ → PGL(W)}} for {{math|V, W}} finite-dimensional vector spaces are faithful.
It follows that the center of {{math|SO(3; 1)+}} is trivial, and this excludes the third case. The conclusion is that every representation {{math|Π : SO(3; 1)+ → GL(V)}} and every projective representation {{math|Π : SO(3; 1)+ → PGL(W)}} for {{math|V, W}} finite-dimensional vector spaces are faithful.
By using the fundamental Lie correspondence, the statements and the reasoning above translate directly to Lie algebras with (abelian) nontrivial non-discrete normal subgroups replaced by (one-dimensional) nontrivial ideals in the Lie algebra,[127] and the center of {{math|SO(3; 1)+}} replaced by the center of 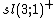 The center of any semisimple Lie algebra is trivial[128] and
The center of any semisimple Lie algebra is trivial[128] and  is semi-simple and simple, and hence has no non-trivial ideals.
is semi-simple and simple, and hence has no non-trivial ideals.
A related fact is that if the corresponding representation of  is faithful, then the representation is projective. Conversely, if the representation is non-projective, then the corresponding
is faithful, then the representation is projective. Conversely, if the representation is non-projective, then the corresponding  representation is not faithful, but is {{math|2:1}}.
representation is not faithful, but is {{math|2:1}}.
Non-unitarity
The {{math|(m, n)}} Lie algebra representation is not Hermitian. Accordingly, the corresponding (projective) representation of the group is never unitary.[129] This is due to the non-compactness of the Lorentz group. In fact, a connected simple non-compact Lie group cannot have any nontrivial unitary finite-dimensional representations.[51] There is a topological proof of this.[130] Let {{math|u : G → GL(V)}}, where {{math|V}} is finite-dimensional, be a continuous unitary representation of the non-compact connected simple Lie group {{mvar|G}}. Then {{math|u(G) ⊂ U(V) ⊂ GL(V)}} where {{math|U(V)}} is the compact subgroup of {{math|GL(V)}} consisting of unitary transformations of {{mvar|V}}. The kernel of {{math|u}} is a normal subgroup of {{mvar|G}}. Since {{mvar|G}} is simple, {{math|ker u}} is either all of {{mvar|G}}, in which case {{math|u}} is trivial, or {{math|ker u}} is trivial, in which case {{math|u}} is faithful. In the latter case {{math|u}} is a diffeomorphism onto its image,[131] {{math|u(G) ≅ G}} and {{math|u(G)}} is a Lie group. This would mean that {{math|u(G)}} is an embedded non-compact Lie subgroup of the compact group {{math|U(V)}}. This is impossible with the subspace topology on {{math|u(G) ⊂ U(V)}} since all embedded Lie subgroups of a Lie group are closed[132] If {{math|u(G)}} were closed, it would be compact,[133] and then {{mvar|G}} would be compact,[134] contrary to assumption.[135]
In the case of the Lorentz group, this can also be seen directly from the definitions. The representations of {{math|A}} and {{math|B}} used in the construction are Hermitian. This means that {{math|J}} is Hermitian, but {{math|K}} is anti-Hermitian.[136] The non-unitarity is not a problem in quantum field theory, since the objects of concern are not required to have a Lorentz-invariant positive definite norm.[137]
Restriction to SO(3)
The {{math|(m, n)}} representation is, however, unitary when restricted to the rotation subgroup {{math|SO(3)}}, but these representations are not irreducible as representations of SO(3). A Clebsch–Gordan decomposition can be applied showing that an {{math|(m, n)}} representation have {{math|SO(3)}}-invariant subspaces of highest weight (spin) {{math|m + n, m + n − 1, … , {{abs| m − n}}}},[138] where each possible highest weight (spin) occurs exactly once. A weight subspace of highest weight (spin) {{math|j}} is {{math|(2j + 1)}}-dimensional. So for example, the ({{sfrac|1|2}}, {{sfrac|1|2}}) representation has spin 1 and spin 0 subspaces of dimension 3 and 1 respectively.
Since the angular momentum operator is given by {{math|J {{=}} A + B}}, the highest spin in quantum mechanics of the rotation sub-representation will be {{math|(m + n)ℏ}} and the "usual" rules of addition of angular momenta and the formalism of 3-j symbols, 6-j symbols, etc. applies.[139]
Spinors
It is the {{math|SO(3)}}-invariant subspaces of the irreducible representations that determine whether a representation has spin. From the above paragraph, it is seen that the {{math|(m, n)}} representation has spin if {{math|m + n}} is half-integral. The simplest are {{math|( {{sfrac|1|2}}, 0)}} and {{math|(0, {{sfrac|1|2}})}}, the Weyl-spinors of dimension {{math|2}}. Then, for example, {{math|(0, {{sfrac|3|2}})}} and {{math|(1, {{sfrac|1|2}})}} are a spin representations of dimensions {{math|2{{sfrac|3|2}} + 1 {{=}} 4}} and {{math|(2 + 1)(2{{sfrac|1|2}} + 1) {{=}} 6}} respectively. Note that, according to the above paragraph, there are subspaces with spin both {{math|{{sfrac|3|2}}}} and {{math|{{sfrac|1|2}}}} in the last two cases, so these representations cannot likely represent a single physical particle which must be well-behaved under {{math|SO(3)}}. It cannot be ruled out in general, however, that representations with multiple {{math|SO(3)}} subrepresentations with different spin can represent physical particles with well-defined spin. It may be that there is a suitable relativistic wave equation that projects out unphysical components, leaving only a single spin.[140]
Construction of pure spin {{math|{{sfrac|n|2}}}} representations for any {{math|n}} (under {{math|SO(3)}}) from the irreducible representations involves taking tensor products of the Dirac-representation with a non-spin representation, extraction of a suitable subspace, and finally imposing differential constraints.[141]
Dual representations
The following theorems are applied to examine whether the dual representation of an irreducible representation is isomorphic to the original representation:
- The set of weights of the dual representation of an irreducible representation of a semisimple Lie algebra is, including multiplicities, the negative of the set of weights for the original representation.&91;142&93;
- Two irreducible representations are isomorphic if and only if they have the same highest weight.&91;143&93;
- For each semisimple Lie algebra there exists a unique element {{math|w0}} of the Weyl group such that if {{math|μ}} is a dominant integral weight, then {{math|w0 ⋅ (−μ)}} is again a dominant integral weight.&91;144&93;
- If
 is an irreducible representation with highest weight {{math|μ0}}, then
is an irreducible representation with highest weight {{math|μ0}}, then  has highest weight {{math|w0 ⋅ (−μ)}}.&91;144&93;
has highest weight {{math|w0 ⋅ (−μ)}}.&91;144&93;
Here, the elements of the Weyl group are considered as orthogonal transformations, acting by matrix multiplication, on the real vector space of roots. If {{math|−I}} is an element of the Weyl group of a semisimple Lie algebra, then {{math|w0 {{=}} −I}}. In the case of 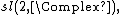 the Weyl group is {{math|W {{=}} {I, −I}
the Weyl group is {{math|W {{=}} {I, −I}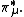 The root system of
The root system of 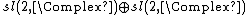 is shown in the figure to the right.[146] The Weyl group is generated by
is shown in the figure to the right.[146] The Weyl group is generated by  where
where 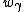 is reflection in the plane orthogonal to {{math|γ}} as {{math|γ}} ranges over all roots.[147] Inspection shows that {{math|wα ⋅ wβ {{=}} −I}} so {{math|−I ∈ W}}. Using the fact that if {{math|π, σ}} are Lie algebra representations and {{math|π ≅ σ}}, then {{math|Π ≅ Σ}},[148] the conclusion for {{math|SO(3; 1)+}} is
is reflection in the plane orthogonal to {{math|γ}} as {{math|γ}} ranges over all roots.[147] Inspection shows that {{math|wα ⋅ wβ {{=}} −I}} so {{math|−I ∈ W}}. Using the fact that if {{math|π, σ}} are Lie algebra representations and {{math|π ≅ σ}}, then {{math|Π ≅ Σ}},[148] the conclusion for {{math|SO(3; 1)+}} is
Complex conjugate representations
If {{math|π}} is a representation of a Lie algebra, then 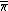 is a representation, where the bar denotes entry-wise complex conjugation in the representative matrices. This follows from that complex conjugation commutes with addition and multiplication.[149] In general, every irreducible representation {{math|π}} of
is a representation, where the bar denotes entry-wise complex conjugation in the representative matrices. This follows from that complex conjugation commutes with addition and multiplication.[149] In general, every irreducible representation {{math|π}} of  can be written uniquely as {{math|π {{=}} π+ + π−}}, where[150]
can be written uniquely as {{math|π {{=}} π+ + π−}}, where[150]
with 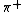 holomorphic (complex linear) and
holomorphic (complex linear) and 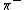 anti-holomorphic (conjugate linear). For
anti-holomorphic (conjugate linear). For 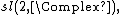 since
since  is holomorphic,
is holomorphic, 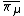 is anti-holomorphic. Direct examination of the explicit expressions for
is anti-holomorphic. Direct examination of the explicit expressions for 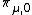 and
and  in equation {{EquationNote|S8|(S8)}} below shows that they are holomorphic and anti-holomorphic respectively. Closer examination of the expression {{EquationNote|S8|(S8)}} also allows for identification of
in equation {{EquationNote|S8|(S8)}} below shows that they are holomorphic and anti-holomorphic respectively. Closer examination of the expression {{EquationNote|S8|(S8)}} also allows for identification of 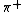 and
and 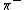 for
for  as
as
Using the above identities (interpreted as pointwise addition of functions), for {{math|SO(3; 1)+}} yields
where the statement for the group representations follow from {{math|exp({{overline|X}})}} = {{math|{{overline|exp(X)}}}}. It follows that the irreducible representations {{math|(m, n)}} have real matrix representatives if and only if {{math|m {{=}} n}}. Reducible representations on the form {{math|(m, n) ⊕ (n, m)}} have real matrices too.
The adjoint representation, the Clifford algebra, and the Dirac spinor representation
In general representation theory, if {{math|(π, V)}} is a representation of a Lie algebra 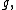 then there is an associated representation of
then there is an associated representation of 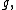 on {{math|End(V)}}, also denoted {{mvar|π}}, given by
on {{math|End(V)}}, also denoted {{mvar|π}}, given by
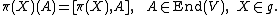 |{{EquationRef|I1|I1}}}}
|{{EquationRef|I1|I1}}}}Likewise, a representation {{math|(Π, V)}} of a group {{mvar|G}} yields a representation {{math|Π}} on {{math|End(V)}} of {{mvar|G}}, still denoted {{math|Π}}, given by[151]
{{NumBlk|:| |{{EquationRef|I2|I2}}}}
|{{EquationRef|I2|I2}}}}If {{mvar|π}} and {{math|Π}} are the standard representations on  and if the action is restricted to
and if the action is restricted to  then the two above representations are the adjoint representation of the Lie algebra and the adjoint representation of the group respectively. The corresponding representations (some
then the two above representations are the adjoint representation of the Lie algebra and the adjoint representation of the group respectively. The corresponding representations (some  or
or 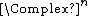 ) always exist for any matrix Lie group, and are paramount for investigation of the representation theory in general, and for any given Lie group in particular.
) always exist for any matrix Lie group, and are paramount for investigation of the representation theory in general, and for any given Lie group in particular.
Applying this to the Lorentz group, if {{math|(Π, V)}} is a projective representation, then direct calculation using {{EquationNote|G5|(G5)}} shows that the induced representation on {{math|End(V)}} is a proper representation, i.e. a representation without phase factors.
In quantum mechanics this means that if {{math|(π, H)}} or {{math|(Π, H)}} is a representation acting on some Hilbert space {{mvar|H}}, then the corresponding induced representation acts on the set of linear operators on {{mvar|H}}. As an example, the induced representation of the projective spin {{math|({{sfrac|1|2}}, 0) ⊕ (0, {{sfrac|1|2}})}} representation on {{math|End(H)}} is the non-projective 4-vector ({{sfrac|1|2}}, {{sfrac|1|2}}) representation.[152]
For simplicity, consider only the "discrete part" of {{math|End(H)}}, that is, given a basis for {{mvar|H}}, the set of constant matrices of various dimension, including possibly infinite dimensions. The induced 4-vector representation of above on this simplified {{math|End(H)}} has an invariant 4-dimensional subspace that is spanned by the four gamma matrices.[153] (The metric convention is different in the linked article.) In a corresponding way, the complete Clifford algebra of spacetime,  whose complexification is
whose complexification is 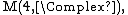 generated by the gamma matrices decomposes as a direct sum of representation spaces of a scalar irreducible representation (irrep), the {{math|(0, 0)}}, a pseudoscalar irrep, also the {{math|(0, 0)}}, but with parity inversion eigenvalue {{math|−1}}, see the next section below, the already mentioned vector irrep, {{math|({{sfrac|1|2}}, {{sfrac|1|2}})}}, a pseudovector irrep, {{math|({{sfrac|1|2}}, {{sfrac|1|2}})}} with parity inversion eigenvalue +1 (not −1), and a tensor irrep, {{math|(1, 0) ⊕ (0, 1)}}.[154] The dimensions add up to {{math|1=1 + 1 + 4 + 4 + 6 = 16}}. In other words,
generated by the gamma matrices decomposes as a direct sum of representation spaces of a scalar irreducible representation (irrep), the {{math|(0, 0)}}, a pseudoscalar irrep, also the {{math|(0, 0)}}, but with parity inversion eigenvalue {{math|−1}}, see the next section below, the already mentioned vector irrep, {{math|({{sfrac|1|2}}, {{sfrac|1|2}})}}, a pseudovector irrep, {{math|({{sfrac|1|2}}, {{sfrac|1|2}})}} with parity inversion eigenvalue +1 (not −1), and a tensor irrep, {{math|(1, 0) ⊕ (0, 1)}}.[154] The dimensions add up to {{math|1=1 + 1 + 4 + 4 + 6 = 16}}. In other words,
 |{{EquationRef|I3|I3}}}}
|{{EquationRef|I3|I3}}}}where, as is customary, a representation is confused with its representation space.
The {{math|({{sfrac|1|2}}, 0) ⊕ (0, {{sfrac|1|2}})}} spin representation
The six-dimensional representation space of the tensor {{math|(1, 0) ⊕ (0, 1)}}-representation inside 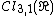 has two roles. The[155]
has two roles. The[155]
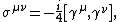 |{{EquationRef|I4|I4}}}}
|{{EquationRef|I4|I4}}}}where 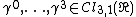 are the gamma matrices, the sigmas, only {{math|6}} of which are non-zero due to antisymmetry of the bracket, span the tensor representation space. Moreover, they have the commutation relations of the Lorentz Lie algebra,[156]
are the gamma matrices, the sigmas, only {{math|6}} of which are non-zero due to antisymmetry of the bracket, span the tensor representation space. Moreover, they have the commutation relations of the Lorentz Lie algebra,[156]
 |{{EquationRef|I5|I5}}}}
|{{EquationRef|I5|I5}}}}and hence constitute a representation (in addition to spanning a representation space) sitting inside  the {{math|({{sfrac|1|2}}, 0) ⊕ (0, {{sfrac|1|2}})}} spin representation. For details, see bispinor and Dirac algebra.
the {{math|({{sfrac|1|2}}, 0) ⊕ (0, {{sfrac|1|2}})}} spin representation. For details, see bispinor and Dirac algebra.
The conclusion is that every element of the complexified 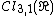 in {{math|End(H)}} (i.e. every complex {{gaps|4|×|4}} matrix) has well defined Lorentz transformation properties. In addition, it has a spin-representation of the Lorentz Lie algebra, which upon exponentiation becomes a spin representation of the group, acting on
in {{math|End(H)}} (i.e. every complex {{gaps|4|×|4}} matrix) has well defined Lorentz transformation properties. In addition, it has a spin-representation of the Lorentz Lie algebra, which upon exponentiation becomes a spin representation of the group, acting on 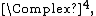 making it a space of bispinors.
making it a space of bispinors.
Reducible representations
There is a multitude of other representations that can be deduced from the irreducible ones, such as those obtained by taking direct sums, tensor products, and quotients of the irreducible representations. Other methods of obtaining representations include the restriction of a representation of a larger group containing the Lorentz group, e.g. 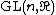 and the Poincaré group. These representations are in general not irreducible.
and the Poincaré group. These representations are in general not irreducible.
The Lorentz group and its Lie algebra have the complete reducibility property. This means that every representation reduces to a direct sum of irreducible representations. The reducible representations will therefore not be discussed.
Space inversion and time reversal
The (possibly projective) {{math|(m, n)}} representation is irreducible as a representation {{math|SO(3; 1)+}}, the identity component of the Lorentz group, in physics terminology the proper orthochronous Lorentz group. If {{math|1=m = n}} it can be extended to a representation of all of {{math|O(3; 1)}}, the full Lorentz group, including space parity inversion and time reversal. The representations {{math|(m, n) ⊕ (n, m)}} can be extended likewise.[157]
Space parity inversion
For space parity inversion, the adjoint action {{math|AdP}} of {{math|P ∈ SO(3; 1)}} on  is considered, where {{math|P}} is the standard representative of space parity inversion, {{math|1=P = diag(1, −1, −1, −1)}}, given by
is considered, where {{math|P}} is the standard representative of space parity inversion, {{math|1=P = diag(1, −1, −1, −1)}}, given by
 |{{EquationRef|F1|F1}}}}
|{{EquationRef|F1|F1}}}}It is these properties of {{math|K}} and {{math|J}} under {{mvar|P}} that motivate the terms vector for {{math|K}} and pseudovector or axial vector for {{math|J}}. In a similar way, if {{math|π}} is any representation of  and {{math|Π}} is its associated group representation, then {{math|Π(SO(3; 1)+)}} acts on the representation of {{math|π}} by the adjoint action, {{math|π(X) ↦ Π(g) π(X) Π(g)−1}} for
and {{math|Π}} is its associated group representation, then {{math|Π(SO(3; 1)+)}} acts on the representation of {{math|π}} by the adjoint action, {{math|π(X) ↦ Π(g) π(X) Π(g)−1}} for 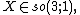 {{math|g ∈ SO(3; 1)+}}. If {{math|P}} is to be included in {{math|Π}}, then consistency with {{EquationNote|F1|(F1)}} requires that
{{math|g ∈ SO(3; 1)+}}. If {{math|P}} is to be included in {{math|Π}}, then consistency with {{EquationNote|F1|(F1)}} requires that
 |{{EquationRef|F2|F2}}}}
|{{EquationRef|F2|F2}}}}holds, where {{math|A}} and {{math|B}} are defined as in the first section. This can hold only if {{math|Ai}} and {{math|Bi}} have the same dimensions, i.e. only if {{math|1=m = n}}. When {{math|m ≠ n}} then {{math|(m, n) ⊕ (n, m)}} can be extended to an irreducible representation of {{math|SO(3; 1)+}}, the orthochronous Lorentz group. The parity reversal representative {{math|Π(P)}} does not come automatically with the general construction of the {{math|(m, n)}} representations. It must be specified separately. The matrix {{math|1=β = i γ0}} (or a multiple of modulus −1 times it) may be used in the {{math|({{sfrac|1|2}}, 0) ⊕ (0, {{sfrac|1|2}})}}[158] representation.
If parity is included with a minus sign (the {{math|1×1}} matrix {{math|[−1]}}) in the {{math|(0,0)}} representation, it is called a pseudoscalar representation.
Time reversal
Time reversal {{math|1=T = diag(−1, 1, 1, 1)}}, acts similarly on by[159]{{NumBlk|:|
by[159]{{NumBlk|:| |{{EquationRef|F3|F3}}}}
|{{EquationRef|F3|F3}}}}By explicitly including a representative for {{math|T}}, as well as one for {{math|P}}, a representation of the full Lorentz group {{math|O(3; 1)}} is obtained. A subtle problem appears however in application to physics, in particular quantum mechanics. When considering the full Poincaré group, four more generators, the {{mvar|Pμ}}, in addition to the {{mvar|Ji}} and {{mvar|Ki}} generate the group. These are interpreted as generators of translations. The time-component {{math|P0}} is the Hamiltonian {{math|H}}. The operator {{math|T}} satisfies the relation[160]
{{NumBlk|:|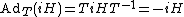 |{{EquationRef|F4|F4}}}}
|{{EquationRef|F4|F4}}}}in analogy to the relations above with  replaced by the full Poincaré algebra. By just cancelling the {{mvar|i}}'s, the result {{math|1=THT−1 = −H}} would imply that for every state {{math|Ψ}} with positive energy {{mvar|E}} in a Hilbert space of quantum states with time-reversal invariance, there would be a state {{math|Π(T−1)Ψ}} with negative energy {{math|−E}}. Such states do not exist. The operator {{math|Π(T)}} is therefore chosen antilinear and antiunitary, so that it anticommutes with {{mvar|i}}, resulting in {{math|THT−1 {{=}} H}}, and its action on Hilbert space likewise becomes antilinear and antiunitary.[161] It may be expressed as the composition of complex conjugation with multiplication by a unitary matrix.[162] This is mathematically sound, see Wigner's theorem, but with very strict requirements on terminology, {{math|Π}} is not a representation.
replaced by the full Poincaré algebra. By just cancelling the {{mvar|i}}'s, the result {{math|1=THT−1 = −H}} would imply that for every state {{math|Ψ}} with positive energy {{mvar|E}} in a Hilbert space of quantum states with time-reversal invariance, there would be a state {{math|Π(T−1)Ψ}} with negative energy {{math|−E}}. Such states do not exist. The operator {{math|Π(T)}} is therefore chosen antilinear and antiunitary, so that it anticommutes with {{mvar|i}}, resulting in {{math|THT−1 {{=}} H}}, and its action on Hilbert space likewise becomes antilinear and antiunitary.[161] It may be expressed as the composition of complex conjugation with multiplication by a unitary matrix.[162] This is mathematically sound, see Wigner's theorem, but with very strict requirements on terminology, {{math|Π}} is not a representation.
When constructing theories such as QED which is invariant under space parity and time reversal, Dirac spinors may be used, while theories that do not, such as the electroweak force, must be formulated in terms of Weyl spinors. The Dirac representation, {{nowrap|({{sfrac|1|2}}, 0) ⊕ (0, {{sfrac|1|2}})}}, is usually taken to include both space parity and time inversions. Without space parity inversion, it is not an irreducible representation.
The third discrete symmetry entering in the CPT theorem along with {{math|P}} and {{math|T}}, charge conjugation symmetry {{math|C}}, has nothing directly to do with Lorentz invariance.[163]
Action on function spaces
If {{mvar|V}} is a vector space of functions of a finite number of variables {{mvar|n}}, then the action on a scalar function 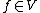 given by
given by
 |{{EquationRef|H1|H1}}}}
|{{EquationRef|H1|H1}}}}produces another function {{math|Πf ∈ V}}. Here {{math|Πx}} is an {{mvar|n}}-dimensional representation, and {{math|Π}} is a possibly infinite-dimensional representation. A special case of this construction is when {{mvar|V}} is a space of functions defined on the a linear group {{mvar|G}} itself, viewed as a {{mvar|n}}-dimensional manifold embedded in  (with {{mvar|m}} the dimension of the matrices).[164] This is the setting in which the Peter–Weyl theorem and the Borel–Weil theorem are formulated. The former demonstrates the existence of a Fourier decomposition of functions on a compact group into characters of finite-dimensional representations.[81] The latter theorem, providing more explicit representations, makes use of the unitarian trick to yield representations of complex non-compact groups, e.g.
(with {{mvar|m}} the dimension of the matrices).[164] This is the setting in which the Peter–Weyl theorem and the Borel–Weil theorem are formulated. The former demonstrates the existence of a Fourier decomposition of functions on a compact group into characters of finite-dimensional representations.[81] The latter theorem, providing more explicit representations, makes use of the unitarian trick to yield representations of complex non-compact groups, e.g. 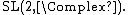
The following exemplifies action of the Lorentz group and the rotation subgroup on some function spaces.
Euclidean rotations
{{Main|Rotation group SO(3)#Spherical harmonics|Spherical harmonics}}The subgroup {{math|SO(3)}} of three-dimensional Euclidean rotations has an infinite-dimensional representation on the Hilbert space
where  are the spherical harmonics. An arbitrary square integrable function {{mvar|f}} one the unit sphere can be expressed as[165]
are the spherical harmonics. An arbitrary square integrable function {{mvar|f}} one the unit sphere can be expressed as[165]
 |{{EquationRef|H2|H2}}}}
|{{EquationRef|H2|H2}}}}where the {{math|flm}} are generalized Fourier coefficients.
The Lorentz group action restricts to that of {{math|SO(3)}} and is expressed as
{{NumBlk|:| |{{EquationRef|H4|H4}}}}
|{{EquationRef|H4|H4}}}}where the {{math|Dl}} are obtained from the representatives of odd dimension of the generators of rotation.
The Möbius group
{{Main|Möbius transformation|Lorentz group#Relation to the Möbius group}}The identity component of the Lorentz group is isomorphic to the Möbius group {{math|M}}. This group can be thought of as conformal mappings of either the complex plane or, via stereographic projection, the Riemann sphere. In this way, the Lorentz group itself can be thought of as acting conformally on the complex plane or on the Riemann sphere.
In the plane, a Möbius transformation characterized by the complex numbers {{math|a, b, c, d}} acts on the plane according to[166]
{{NumBlk|:| .|{{EquationRef|M1|M1}}}}
.|{{EquationRef|M1|M1}}}}and can be represented by complex matrices
{{NumBlk|:|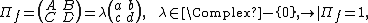 |{{EquationRef|M2|M2}}}}
|{{EquationRef|M2|M2}}}}since multiplication by a nonzero complex scalar does not change {{mvar|f}}. These are elements of  and are unique up to a sign (since {{math|±Πf}} give the same {{mvar|f}}), hence
and are unique up to a sign (since {{math|±Πf}} give the same {{mvar|f}}), hence 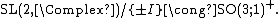
The Riemann P-functions
{{Main|Riemann's differential equation}}The Riemann P-functions, solutions of Riemann's differential equation, are an example of a set of functions that transform among themselves under the action of the Lorentz group. The Riemann P-functions are expressed as[167]
{{NumBlk|||{{EquationRef|T1|T1}}}}
where the {{math|a, b, c, α, β, γ, α′, β′, γ′}} are complex constants. The P-function on the right hand side can be expressed using standard hypergeometric functions. The connection is[168]
{{NumBlk|:| |{{EquationRef|T2|T2}}}}
|{{EquationRef|T2|T2}}}}The set of constants {{math|0, ∞, 1}} in the upper row on the left hand side are the regular singular points of the Gauss' hypergeometric equation.[169] Its exponents, i. e. solutions of the indicial equation, for expansion around the singular point {{math|0}} are {{math|0}} and {{math|1 − c}} ,corresponding to the two linearly independent solutions,[170] and for expansion around the singular point {{math|1}} they are {{math|0}} and {{math|c − a − b}}.[171] Similarly, the exponents for {{math|∞}} are {{mvar|a}} and {{mvar|b}} for the two solutions.[172]
One has thus
{{NumBlk|:|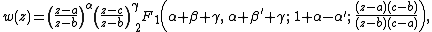 |{{EquationRef|T3|T3}}}}
|{{EquationRef|T3|T3}}}}where the condition (sometimes called Riemann's identity)[173]
on the exponents of the solutions of Riemann's differential equation has been used to define {{math|γ′}}.
The first set of constants on the left hand side in {{EquationNote|T1|(T1)}}, {{math|a, b, c}} denotes the regular singular points of Riemann's differential equation. The second set, {{math|α, β, γ}}, are the corresponding exponents at {{math|a, b, c}} for one of the two linearly independent solutions, and, accordingly, {{math|α′, β′, γ′}} are exponents at {{math|a, b, c}} for the second solution.
Define an action of the Lorentz group on the set of all Riemann P-functions by first setting
{{NumBlk|:|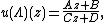 |{{EquationRef|T4|T4}}}}
|{{EquationRef|T4|T4}}}}where {{math|A, B, C, D}} are the entries in
{{NumBlk|:|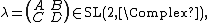 |{{EquationRef|T5|T5}}}}
|{{EquationRef|T5|T5}}}}for {{math|Λ {{=}} p(λ) ∈ SO(3; 1)+}} a Lorentz transformation.
Define
{{NumBlk|:|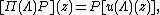 |{{EquationRef|T6|T6}}}}
|{{EquationRef|T6|T6}}}}where {{mvar|P}} is a Riemann P-function. The resulting function is again a Riemann P-function. The effect of the Möbius transformation of the argument is that of shifting the poles to new locations, hence changing the critical points, but there is no change in the exponents of the differential equation the new function satisfies. The new function is expressed as
{{NumBlk|:| |{{EquationRef|T6|T6}}}}
|{{EquationRef|T6|T6}}}}where
{{NumBlk|:| |{{EquationRef|T7|T7}}}}
|{{EquationRef|T7|T7}}}}==Infinite-dimensional unitary representations==
History
The Lorentz group {{math|SO(3; 1)+}} and its double cover  also have infinite dimensional unitary representations, studied independently by {{harvtxt|Bargmann|1947}}, {{harvtxt|Gelfand|Naimark|1947}} and {{harvtxt|Harish-Chandra|1947}} at the instigation of Paul Dirac.[174][175] This trail of development begun with {{harvtxt|Dirac|1936}} where he devised matrices {{math|U}} and {{math|B}} necessary for description of higher spin (compare Dirac matrices), elaborated upon by {{harvtxt|Fierz|1939}}, see also {{harvtxt|Fierz|Pauli|1939}}, and proposed precursors of the Bargmann-Wigner equations.[176] In {{harvtxt|Dirac|1945}} he proposed a concrete infinite-dimensional representation space whose elements were called expansors as a generalization of tensors.[177] These ideas were incorporated by Harish–Chandra and expanded with expinors as an infinite-dimensional generalization of spinors in his 1947 paper.
also have infinite dimensional unitary representations, studied independently by {{harvtxt|Bargmann|1947}}, {{harvtxt|Gelfand|Naimark|1947}} and {{harvtxt|Harish-Chandra|1947}} at the instigation of Paul Dirac.[174][175] This trail of development begun with {{harvtxt|Dirac|1936}} where he devised matrices {{math|U}} and {{math|B}} necessary for description of higher spin (compare Dirac matrices), elaborated upon by {{harvtxt|Fierz|1939}}, see also {{harvtxt|Fierz|Pauli|1939}}, and proposed precursors of the Bargmann-Wigner equations.[176] In {{harvtxt|Dirac|1945}} he proposed a concrete infinite-dimensional representation space whose elements were called expansors as a generalization of tensors.[177] These ideas were incorporated by Harish–Chandra and expanded with expinors as an infinite-dimensional generalization of spinors in his 1947 paper.
The Plancherel formula for these groups was first obtained by Gelfand and Naimark through involved calculations. The treatment was subsequently considerably simplified by {{harvtxt|Harish-Chandra|1951}} and {{harvtxt|Gelfand|Graev|1953}}, based on an analogue for  of the integration formula of Hermann Weyl for compact Lie groups.[178] Elementary accounts of this approach can be found in {{harvtxt|Rühl|1970}} and {{harvtxt|Knapp|2001}}.
of the integration formula of Hermann Weyl for compact Lie groups.[178] Elementary accounts of this approach can be found in {{harvtxt|Rühl|1970}} and {{harvtxt|Knapp|2001}}.
The theory of spherical functions for the Lorentz group, required for harmonic analysis on the hyperboloid model of 3-dimensional hyperbolic space sitting in Minkowski space is considerably easier than the general theory. It only involves representations from the spherical principal series and can be treated directly, because in radial coordinates the Laplacian on the hyperboloid is equivalent to the Laplacian on 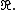 This theory is discussed in {{harvtxt|Takahashi|1963}}, {{harvtxt|Helgason|1968}}, {{harvtxt|Helgason|2000}} and the posthumous text of {{harvtxt|Jorgenson|Lang|2008}}.
This theory is discussed in {{harvtxt|Takahashi|1963}}, {{harvtxt|Helgason|1968}}, {{harvtxt|Helgason|2000}} and the posthumous text of {{harvtxt|Jorgenson|Lang|2008}}.
Principal series for SL(2, C)
The principal series, or unitary principal series, are the unitary representations induced from the one-dimensional representations of the lower triangular subgroup {{mvar|B}} of  Since the one-dimensional representations of {{mvar|B}} correspond to the representations of the diagonal matrices, with non-zero complex entries {{mvar|z}} and {{math|z−1}}, they thus have the form
Since the one-dimensional representations of {{mvar|B}} correspond to the representations of the diagonal matrices, with non-zero complex entries {{mvar|z}} and {{math|z−1}}, they thus have the form
for {{mvar|k}} an integer, {{mvar|ν}} real and with {{mvar|1=z = reiθ}}. The representations are irreducible; the only repetitions, i.e. isomorphisms of representations, occur when {{mvar|k}} is replaced by {{math|−k}}. By definition the representations are realized on {{math|L2}} sections of line bundles on  which is isomorphic to the Riemann sphere. When {{math|1=k = 0}}, these representations constitute the so-called spherical principal series.
which is isomorphic to the Riemann sphere. When {{math|1=k = 0}}, these representations constitute the so-called spherical principal series.
The restriction of a principal series to the maximal compact subgroup {{math|1=K = SU(2)}} of {{mvar|G}} can also be realized as an induced representation of {{mvar|K}} using the identification {{math|1=G/B = K/T}}, where {{math|1=T = B ∩ K}} is the maximal torus in {{mvar|K}} consisting of diagonal matrices with {{math|1={{!}} z {{!}} = 1}}. It is the representation induced from the 1-dimensional representation {{math|zkT}}, and is independent of {{mvar|ν}}. By Frobenius reciprocity, on {{mvar|K}} they decompose as a direct sum of the irreducible representations of {{mvar|K}} with dimensions {{math|1={{abs|k}} + 2m + 1}} with {{mvar|m}} a non-negative integer.
Using the identification between the Riemann sphere minus a point and  the principal series can be defined directly on
the principal series can be defined directly on  by the formula[179]
by the formula[179]
|cellpadding=6|border|border colour=#0073CF|bgcolor=#F9FFF7}}
Irreducibility can be checked in a variety of ways:
- The representation is already irreducible on {{mvar|B}}. This can be seen directly, but is also a special case of general results on irreducibility of induced representations due to François Bruhat and George Mackey, relying on the Bruhat decomposition {{math|1=G = B ∪ BsB}} where {{mvar|s}} is the Weyl group element[180]
.
- The action of the Lie algebra
 of {{mvar|G}} can be computed on the algebraic direct sum of the irreducible subspaces of {{mvar|K}} can be computed explicitly and the it can be verified directly that the lowest-dimensional subspace generates this direct sum as a
of {{mvar|G}} can be computed on the algebraic direct sum of the irreducible subspaces of {{mvar|K}} can be computed explicitly and the it can be verified directly that the lowest-dimensional subspace generates this direct sum as a  -module.[181][182]
-module.[181][182]
Complementary series for SL(2, C)
The for {{math|0 < t < 2}}, the complementary series is defined on 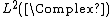 for the inner product[183]
for the inner product[183]
with the action given by[184][185]
{{Equation box 1|indent=|equation=|cellpadding=6|border|border colour=#0073CF|bgcolor=#F9FFF7}}
The representations in the complementary series are irreducible and pairwise non-isomorphic. As a representation of {{mvar|K}}, each is isomorphic to the Hilbert space direct sum of all the odd dimensional irreducible representations of {{math|1=K = SU(2)}}. Irreducibility can be proved by analyzing the action of  on the algebraic sum of these subspaces[181][182] or directly without using the Lie algebra.[186][187]
on the algebraic sum of these subspaces[181][182] or directly without using the Lie algebra.[186][187]
Plancherel theorem for SL(2, C)
The only irreducible unitary representations of  are the principal series, the complementary series and the trivial representation.
are the principal series, the complementary series and the trivial representation.
Since {{math|−I}} acts as {{math|(−1)k}} on the principal series and trivially on the remainder, these will give all the irreducible unitary representations of the Lorentz group, provided {{mvar|k}} is taken to be even.
To decompose the left regular representation of {{mvar|G}} on 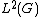 only the principal series are required. This immediately yields the decomposition on the subrepresentations
only the principal series are required. This immediately yields the decomposition on the subrepresentations 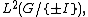 the left regular representation of the Lorentz group, and
the left regular representation of the Lorentz group, and  the regular representation on 3-dimensional hyperbolic space. (The former only involves principal series representations with k even and the latter only those with {{math|1=k = 0}}.)
the regular representation on 3-dimensional hyperbolic space. (The former only involves principal series representations with k even and the latter only those with {{math|1=k = 0}}.)
The left and right regular representation {{mvar|λ}} and {{mvar|ρ}} are defined on  by
by
Now if {{mvar|f}} is an element of {{math|Cc(G)}}, the operator  defined by
defined by
is Hilbert–Schmidt. Define a Hilbert space {{mvar|H}} by
where
and  denotes the Hilbert space of Hilbert–Schmidt operators on
denotes the Hilbert space of Hilbert–Schmidt operators on  [188] Then the map {{mvar|U}} defined on {{math|Cc(G)}} by
[188] Then the map {{mvar|U}} defined on {{math|Cc(G)}} by
extends to a unitary of 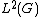 onto {{mvar|H}}.
onto {{mvar|H}}.
The map {{mvar|U}} satisfies the intertwining property
If {{math|f1, f2}} are in {{math|Cc(G)}} then by unitarity
{{Equation box 1| cellpadding=6
| border | border colour=#0073CF
| bgcolor=#F9FFF7
| indent=:
| equation=
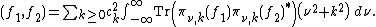
}}
Thus if 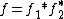 denotes the convolution of
denotes the convolution of  and
and  and
and 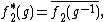 then[189]
then[189]
| cellpadding=6
| border | border colour=#0073CF
| bgcolor=#F9FFF7
| indent=:
| equation=

}}
The last two displayed formulas are usually referred to as the Plancherel formula and the Fourier inversion formula respectively.
The Plancherel formula extends to all 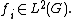 By a theorem of Jacques Dixmier and Paul Malliavin, every smooth compactly supported function on
By a theorem of Jacques Dixmier and Paul Malliavin, every smooth compactly supported function on  is a finite sum of convolutions of similar functions, the inversion formula holds for such {{mvar|f}}. It can be extended to much wider classes of functions satisfying mild differentiability conditions.[81]
is a finite sum of convolutions of similar functions, the inversion formula holds for such {{mvar|f}}. It can be extended to much wider classes of functions satisfying mild differentiability conditions.[81]
Classification of representations of SO(3, 1)
The strategy followed in the classification of the irreducible infinite-dimensional representations is, in analogy to the finite-dimensional case, to assume they exist, and to investigate their properties. Thus first assume that an irreducible strongly continuous infinite-dimensional representation {{math|ΠH}} on a Hilbert space {{mvar|H}} of {{math|SO(3; 1)+}} is at hand.[190] Since {{math|SO(3)}} is a subgroup, {{math|ΠH}} is a representation of it as well. Each irreducible subrepresentation of {{math|SO(3)}} is finite-dimensional, and the {{math|SO(3)}} representation is reducible into a direct sum of irreducible finite-dimensional unitary representations of {{math|SO(3)}} if {{math|ΠH}} is unitary.[191]
The steps are the following:[192]
- Chose a suitable basis of common eigenvectors of {{math|J2}} and {{math|J3}}.
- Compute matrix elements of {{math|J1, J2, J3}} and {{math|K1, K2, K3}}.
- Enforce Lie algebra commutation relations.
- Require unitarity together with orthonormality of the basis.&91;193&93;
Step 1
One suitable choice of basis and labeling is given by
If this were a finite-dimensional representation, then {{math|j0}} would correspond the lowest occurring eigenvalue {{math|j(j + 1)}} of {{math|J2}} in the representation, equal to {{math|{{!}}m − n{{!}}}}, and {{math|j1}} would correspond to the highest occurring eigenvalue, equal to {{math|m + n}}. In the infinite-dimensional case, {{math|j0 ≥ 0}} retains this meaning, but {{math|j1}} does not.[90] For simplicity, it is assumed that a given {{mvar|j}} occurs at most once in a given representation (this is the case for finite-dimensional representations), and it can be shown[194] that the assumption is possible to avoid (with a slightly more complicated calculation) with the same results.
Step 2
The next step is to compute the matrix elements of the operators {{math|J1, J2, J3}} and {{math|K1, K2, K3}} forming the basis of the Lie algebra of  The matrix elements of
The matrix elements of 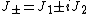 and
and  (the complexified Lie algebra is understood) are known from the representation theory of the rotation group, and are given by[195][196]
(the complexified Lie algebra is understood) are known from the representation theory of the rotation group, and are given by[195][196]
where the labels {{math|j0}} and {{math|j1}} have been dropped since they are the same for all basis vectors in the representation.
Due to the commutation relations
the triple {{math|(Ki, Ki, Ki) ≡ K}} is a vector operator[197] and the Wigner–Eckart theorem[198] applies for computation of matrix elements between the states represented by the chosen basis.[199] The matrix elements of
where the superscript {{math|(1)}} signifies that the defined quantities are the components of a spherical tensor operator of rank {{math|k {{=}} 1}} (which explains the factor {{math|{{sqrt|2}}}} as well) and the subscripts {{math|0, ±1}} are referred to as {{mvar|q}} in formulas below, are given by[200]
Here the first factors on the right hand sides are Clebsch–Gordan coefficients for coupling {{math|j′}} with {{mvar|k}} to get {{mvar|j}}. The second factors are the reduced matrix elements. They do not depend on {{math|m, m′}} or {{mvar|q}}, but depend on {{math|j, j′}} and, of course, {{math|K}}. For a complete list of non-vanishing equations, see {{harvtxt|Harish-Chandra|1947|p=375}}.
Step 3
The next step is to demand that the Lie algebra relations hold, i.e. that
This results in a set of equations[201] for which the solutions are[202]
where
Step 4
The imposition of the requirement of unitarity of the corresponding representation of the group restricts the possible values for the arbitrary complex numbers {{math|j0}} and {{math|ξj}}. Unitarity of the group representation translates to the requirement of the Lie algebra representatives being Hermitian, meaning
This translates to[203]
leading to[204]
where {{math|βj}} is the angle of {{math|Bj}} on polar form. For {{math|{{!}}Bj{{!}} ≠ 0}} follows  and
and  is chosen by convention. There are two possible cases:
is chosen by convention. There are two possible cases:
-
 In this case {{math|j1 {{=}} − iν}}, {{mvar|ν}} real,[205]
In this case {{math|j1 {{=}} − iν}}, {{mvar|ν}} real,[205]
This is the principal series. Its elements are denoted
-
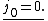 It follows:[206]
It follows:[206]
Since {{math|B0 {{=}} Bj0}}, {{math|B{{supsub|2|j}}}} is real and positive for {{math|j {{=}} 1, 2, ...}} , leading to {{math|−1 ≤ ν ≤ 1}}. This is complementary series. Its elements are denoted {{math|(0, ν), −1 ≤ ν ≤ 1}}.
This shows that the representations of above are all infinite-dimensional irreducible unitary representations.
Explicit formulas
Conventions and Lie algebra bases
The metric of choice is given by {{math|η {{=}} diag(−1, 1, 1, 1)}}, and the physics convention for Lie algebras and the exponential mapping is used. These choices are arbitrary, but once they are made, fixed. One possible choice of basis for the Lie algebra is, in the 4-vector representation, given by:
The commutation relations of the Lie algebra  are:[207]
are:[207]
In three-dimensional notation, these are[208]
The choice of basis above satisfies the relations, but other choices are possible. The multiple use of the symbol {{mvar|J}} above and in the sequel should be observed.
Weyl spinors and bispinors
By taking, in turn, {{math|m {{=}} {{sfrac|1|2}}, n {{=}} 0}} and {{math|m {{=}} 0, n {{=}} {{sfrac|1|2}}}} and by setting
in the general expression {{EquationNote|G1|(G1)}}, and by using the trivial relations {{math|11 {{=}} 1}} and {{math|J(0) {{=}} 0}}, it follows
{{NumBlk|:
|

| {{EquationRef|W1|W1}}
}}
These are the left-handed and right-handed Weyl spinor representations. They act by matrix multiplication on 2-dimensional complex vector spaces (with a choice of basis) {{math|VL}} and {{math|VR}}, whose elements {{math|ΨL}} and {{math|ΨR}} are called left- and right-handed Weyl spinors respectively. Given
their direct sum as representations is formed,[209]
{{NumBlk|:
|
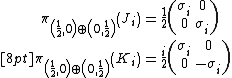
| {{EquationRef|D1|D1}}
}}
This is, up to a similarity transformation, the {{math|({{sfrac|1|2}},0) ⊕ (0,{{sfrac|1|2}})}} Dirac spinor representation of  It acts on the 4-component elements {{math|(ΨL, ΨR)}} of {{math|(VL ⊕ VR)}}, called bispinors, by matrix multiplication. The representation may be obtained in a more general and basis independent way using Clifford algebras. These expressions for bispinors and Weyl spinors all extend by linearity of Lie algebras and representations to all of
It acts on the 4-component elements {{math|(ΨL, ΨR)}} of {{math|(VL ⊕ VR)}}, called bispinors, by matrix multiplication. The representation may be obtained in a more general and basis independent way using Clifford algebras. These expressions for bispinors and Weyl spinors all extend by linearity of Lie algebras and representations to all of  Expressions for the group representations are obtained by exponentiation.
Expressions for the group representations are obtained by exponentiation.
See also
- Bargmann–Wigner equations
- Center of mass (relativistic)
- Dirac algebra
- Gamma matrices
- Lorentz group
- Möbius transformation
- Poincaré group
- Representation theory of the Poincaré group
- Symmetry in quantum mechanics
- Wigner's classification
Remarks
2. ^{{harvnb|Weinberg|2002|p=1}} "If it turned out that a system could not be described by a quantum field theory, it would be a sensation; if it turned out it did not obey the rules of quantum mechanics and relativity, it would be a cataclysm."
3. ^{{harvnb|Bargmann|Wigner|1948}}
4. ^{{harvnb|Bekaert|Boulanger|2006}}
5. ^In 1945 Harish-Chandra came to see Dirac in Cambridge. He became convinced that he was not suitable for theoretical physics. Harish-Chandra had found an error in a proof by Dirac in his work on the Lorentz group. Dirac said "I am not interested in proofs but only interested in what nature does."
Harish-Chandra later wrote "This remark confirmed my growing conviction that I did not have the mysterious sixth sense which one needs in order to succeed in physics and I soon decided to move over to mathematics."
Dirac did however suggest the topic of his thesis, the classification of the irreducible infinite-dimensional representations of the Lorentz group.
See {{harvnb|Dalitz|Peierls|1986}}
6. ^It is tacitly always assumed that each inertial frame has a dedicated Lorentz observer, I. e. someone who has, in principle, a complete record (i. e. coordinates!) of every event as observed in that frame.
7. ^It isn't actually required that the mapping is one-to-one. It is merely required that the mapping is a group homomorphism, i. e. {{math|Π(gh) {{=}} Π(g)Π(h)}} into some {{math|GL(V)}} the general linear group of some vector space {{mvar|V}}. (The vector space {{mvar|V}} is allowed to be infinite-dimensional, e.g a Hilbert space {{math|H}}, in which case one speaks of {{math|B(H)}}, linear operators on {{mvar|H}} instead of {{math|GL(V)}}.
8. ^In an open set of spacetime, there are only two degrees of freedom. Introduction of the four-potential yields nominally four degrees of freedom. The field equations and gauge invariance each remove one degree of freedom.
9. ^This transformation is usually expressed differently, see e.g. transformation of the electromagnetic field. That method can be traced converted to applying a {{math|6 × 6}}-matrix like here and vice versa since the field tensor has {{math|6}} independent components.
10. ^1 {{harvnb|Rossmann|2002|loc=Section 6.1.}}
11. ^There may be representations of uncountable dimension. These are less well behaved (in particular non-unitary) and are not covered here.
12. ^It may happen that the multiplication of two representative infinite-dimensional matrices is ill-defined. The right composition rule can be verified by other means though.
13. ^{{harvnb|Misner|Thorne|Wheeler|1973}}
14. ^{{harvnb|Weinberg|2002|loc=Section 2.5, Chapter 5.}}
15. ^{{harvnb|Tung|1985|loc=Sections 10.3, 10.5.}}
16. ^{{harvnb|Tung|1985|loc=Section 10.4.}}
17. ^{{harvnb|Dirac|1945}}
18. ^{{harvnb|Zwiebach|2004|loc=Section 12.8.}}
19. ^1 {{harvnb|Bekaert|Boulanger|2006|p=48.}}
20. ^{{harvnb|Zwiebach|2004|loc=Section 18.8.}}
21. ^1 {{harvnb|Greiner|Reinhardt|1996|loc=Chapter 2.}}
22. ^{{harvnb|Weinberg|2002|loc=Foreword and introduction to chapter 7.}}
23. ^{{harvnb|Weinberg|2002|loc=Introduction to chapter 7.}}
24. ^{{harvnb|Tung|1985|loc=Definition 10.11.}}
25. ^{{harvtxt|Greiner|Müller|1994|loc=Chapter 1}}
26. ^{{harvtxt|Greiner|Müller|1994|loc=Chapter 2}}
27. ^{{harvnb|Tung|1985|p=203.}}
28. ^{{harvnb|Delbourgo|Salam|Strathdee|1967}}
29. ^{{harvtxt|Weinberg|2002|loc=Section 3.3}}
30. ^See formula (1) in S-matrix#From free particle states for how free multi-particle states transform.
31. ^{{harvtxt|Weinberg|2002|loc=Section 7.4.}}
32. ^{{harvnb|Tung |1985| loc=Introduction to chapter 10.}}
33. ^{{harvnb|Tung|1985|loc=Definition 10.12.}}
34. ^{{harvnb|Tung|1985|loc=Equation 10.5-2.}}
35. ^{{harvnb|Weinberg|2002|loc=Equations 5.1.6–7.}}
36. ^1 {{harvnb|Tung|1985|loc=Equation 10.5–18.}}
37. ^{{harvnb|Weinberg|2002|loc=Equations 5.1.4–5.}} Weinberg deduces the necessity of creation and annihilation operators from another consideration, the cluster decomposition principle, {{harvtxt|Weinberg|2002|loc=Chapter 4.}}
38. ^{{harvnb|Weinberg|2002|loc=Equations 5.1.11–12.}}
39. ^{{harvnb|Tung|1985|loc=Section 10.5.3.}}
40. ^A prescription for how the particle should behave under CPT symmetry may be required as well.
41. ^For instance, there are versions (free field equations, i.e. without interaction terms) of the Klein–Gordon equation, the Dirac equation, the Maxwell equations, the Proca equation, the Rarita–Schwinger equation, and the Einstein field equations that can systematically be deduced by starting from a given representation of the Lorentz group. In general, these are collectively the quantum field theory versions of the Bargmann–Wigner equations.
See {{harvtxt|Weinberg|2002|loc=Chapter 5}}, {{harvtxt|Tung|1985|loc=Section 10.5.2}} and references given in these works.
It should be remarked that high spin theories ({{math|s > 1}}) encounter difficulties. See {{harvtxt|Weinberg|2002|loc=Section 5.8}}, on general {{math|(m, n)}} fields, where this is discussed in some depth, and references therein. High spin particles do without a doubt exist, e.g. nuclei, the known ones are just not elementary.
42. ^For part of their representation theory, see {{harvtxt|Bekaert|Boulanger|2006}}, which is dedicated to representation theory of the Poincare group. These representations are obtained by the method of induced representations or, in physics parlance, the method of the little group, pioneered by Wigner in 1939 for this type of group and put on firm mathematical footing by George Mackey in the fifties.
43. ^{{harvnb|Zwiebach|2004|loc=Section 6.4.}}
44. ^{{harvnb|Zwiebach|2004|loc=Chapter 7.}}
45. ^{{harvnb|Zwiebach|2004|loc=Section 12.5.}}
46. ^1 {{harvnb|Weinberg|2000|loc=Section 25.2.}}
47. ^{{harvnb|Zwiebach|2004|loc=Last paragraph, section 12.6.}}
48. ^These facts can be found in most introductory mathematics and physics texts. See e.g. {{harvtxt|Rossmann|2002}}, {{harvtxt|Hall|2015}} and {{harvtxt|Tung|1985}}.
49. ^{{harvtxt|Hall|2015|loc=Section 4.4.}}{{Paragraph break}}One says that a group has the complete reducibility property if every representation decomposes as a direct sum of irreducible representations.
50. ^{{harvtxt|Hall|2015|loc=Theorem 4.34 and following discussion.}}
51. ^1 2 {{harvnb|Wigner|1939}}
52. ^{{harvnb|Hall|2015|loc=Appendix D2.}}
53. ^{{harvnb|Greiner|Reinhardt|1996}}
54. ^{{harvnb|Weinberg|2002|loc=Section 2.6 and Chapter 5.}}
55. ^1 {{harvnb|Coleman|1989|p=30.}}
56. ^{{harvnb|Lie|1888}}, 1890, 1893. Primary source.
57. ^{{harvnb|Coleman|1989|p=34.}}
58. ^{{harvnb|Killing|1888}} Primary source.
59. ^1 {{harvnb|Rossmann|2002|loc=Historical tidbits scattered across the text.}}
60. ^{{harvnb|Cartan|1913}} Primary source.
61. ^{{harvnb|Green|1998|loc=p=76.}}
62. ^{{harvnb|Brauer|Weyl|1935}} Primary source.
63. ^{{harvnb|Tung|1985|loc=Introduction.}}
64. ^{{harvnb|Weyl|1931}} Primary source.
65. ^{{harvnb|Weyl|1939}} Primary source.
66. ^{{harvnb|Langlands|1985|pp=203–205}}
67. ^{{harvnb|Harish-Chandra|1947}} Primary source.
68. ^{{harvnb|Tung|1985|loc=Introduction}}
69. ^{{harvnb|Wigner|1939}} Primary source.
70. ^{{harvnb|Klauder|1999}}
71. ^{{harvnb|Bargmann|1947}} Primary source.
72. ^Bargmann was also a mathematician. He worked as Albert Einsteins assistant at the Institute for Advanced Study in Princeton ({{harvtxt|Klauder|1999}}).
73. ^{{harvnb|Bargmann|Wigner|1948}} Primary source.
74. ^{{harvnb|Dalitz|Peierls|1986}}
75. ^{{harvnb|Dirac|1928}} Primary source.
76. ^Dirac suggested the topic of {{harvtxt|Wigner|1939}} as early as 1928 (as acknowledged in Wigner's paper). He also published one of the first papers on explicit infinite-dimensional unitary representations in {{harvtxt|Dirac|1945}} ({{harvnb|Langlands|1985}}), and suggested the topic for Harish-Chandra's thesis classifying irreducible infinite-dimensional representations ({{harvnb|Dalitz|Peierls|1986}}).
77. ^{{harvnb|Weinberg|2002|loc=Equations 5.6.7–8.}}
78. ^{{harvnb|Weinberg|2002|loc=Equations 5.6.9–11.}}
79. ^1 2 {{harvnb|Hall|2003|loc=Chapter 6.}}
80. ^{{harvnb|Knapp|2001}} The rather mysterious looking third isomorphism is proved in chapter 2, paragraph 4.
81. ^1 2 {{harvnb|Knapp|2001}}
82. ^This is an application of {{harvnb|Rossmann|2002|loc=Section 6.3, Proposition 10.}}
83. ^Tensor products of representations, {{math|πg ⊗ πh}} of  can, when both factors come from the same Lie algebra
can, when both factors come from the same Lie algebra 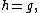 either be thought of as a representation of
either be thought of as a representation of  or
or 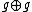 .
.
84. ^When complexifying a complex Lie algebra, it should be thought of as a real Lie algebra of real dimension twice its complex dimension. Likewise, a real form may actually also be complex as is the case here.
85. ^1 {{harvnb|Knapp|2001|p=32.}}
86. ^Combine {{harvtxt|Weinberg|2002|loc=Equations 5.6.7–8, 5.6.14–15}} with {{harvtxt|Hall|2015|loc=Proposition 4.18}} about Lie algebra representations of group tensor product representations.
87. ^{{harvnb|Weinberg|2002|loc=Equations 5.6.16–17.}}
88. ^{{harvnb|Weinberg|2002|loc=Section 5.6.}} The equations follow from equations 5.6.7–8 and 5.6.14–15.
89. ^The "traceless" property can be expressed as {{math|1=Sαβgαβ = 0}}, or {{math|1=Sαα = 0}}, or {{math|1=Sαβgαβ = 0}} depending on the presentation of the field: covariant, mixed, and contravariant respectively.
90. ^1 {{harvnb|Tung|1985}}
91. ^This doesn't necessarily come symmetric directly from the Lagrangian by using Noether's theorem, but it can be symmetrized as the Belinfante–Rosenfeld stress–energy tensor.
92. ^This is provided parity is a symmetry. Else there would be two flavors, {{math|({{sfrac|3|2}}, 0)}} and {{math|(0, {{sfrac|3|2}})}} in analogy with neutrinos.
93. ^{{Harvnb|Weinberg|2002}} See footnote on p. 232.
94. ^{{harvnb|Lie|1888}}
95. ^{{harvnb|Rossmann|2002|loc=Section 2.5.}}
96. ^{{harvnb|Hall|2015|loc=Theorem 2.10.}}
97. ^{{harvnb|Bourbaki|1998|p=424.}}
98. ^{{harvnb|Weinberg|2002|loc=Section 2.7 p.88.}}
99. ^1 2 3 4 {{harvnb|Weinberg|2002|loc=Section 2.7.}}
100. ^{{harvnb|Hall|2015|loc=Appendix C.3.}}
101. ^The terminology differs between mathematics and physics. In the linked article term projective representation has a slightly different meaning than in physics, where a projective representation is though of as a local section (a local inverse) of the covering map from the covering group onto the group being covered, composed with a proper representation of the covering group. Since this can be done (locally) continuously in two ways in the case at hand as explained below, the terminology of a double-valued or two-valued representation is natural.
102. ^{{harvnb|Wigner|1939|p=27.}}
103. ^In particular, {{math|A}} commutes with the Pauli matrices, hence with all of {{math|SU(2)}} making Schur's lemma applicable.
104. ^{{harvnb|Gelfand|Minlos|Shapiro|1963}} This construction of the covering group is treated in paragraph 4, section 1, chapter 1 in Part II.
105. ^Meaning the kernel is trivial, to see this recall that the kernel of a Lie algebra homomorphism is an ideal and hence a subspace. Since {{math|p}} is {{math|2:1}} and both  and {{math|SO(3; 1)+}} are {{nowrap|{{math|6}}-dimensional}}, the kernel must be {{nowrap|{{math|0}}-dimensional}}, hence {{math|{0}.}}
and {{math|SO(3; 1)+}} are {{nowrap|{{math|6}}-dimensional}}, the kernel must be {{nowrap|{{math|0}}-dimensional}}, hence {{math|{0}.}}
106. ^The exponential map is one-to-one in a neighborhood of the identity in  hence the composition
hence the composition  where {{mvar|σ}} is the Lie algebra isomorphism, is onto an open neighborhood {{math|U ⊂ SO(3; 1)+}} containing the identity. Such a neighborhood generates the connected component.
where {{mvar|σ}} is the Lie algebra isomorphism, is onto an open neighborhood {{math|U ⊂ SO(3; 1)+}} containing the identity. Such a neighborhood generates the connected component.
107. ^{{harvnb|Rossmann|2002|loc=Section 2.1.}}
108. ^{{harvnb|Rossmann|2002}} From Example 4 in section 2.1 : This can be seen as follows. The matrix {{mvar|q}} has eigenvalues {{math|{-1, −1} }}, but it is not diagonalizable. If {{math|q {{=}} exp(Q)}}, then {{mvar|Q}} has eigenvalues {{math|λ, −λ}} with {{math|λ {{=}} iπ + 2πik}} for some {{mvar|k}} because elements of  are traceless. But then {{mvar|Q}} is diagonalizable, hence {{mvar|q}} is diagonalizable, which is a contradiction.
are traceless. But then {{mvar|Q}} is diagonalizable, hence {{mvar|q}} is diagonalizable, which is a contradiction.
109. ^{{harvnb|Hall|2015|loc=First displayed equations in section 4.6.}}
110. ^{{harvnb|Hall|2015|loc=Example 4.10.}}
111. ^1 {{harvnb|Knapp|2001|loc=Chapter 2.}}
112. ^{{harvnb|Knapp|2001}} Equation 2.1.
113. ^{{harvnb|Hall|2015|loc=Equation 4.2.}}
114. ^{{harvnb|Hall|2015|loc=Equation before 4.5.}}
115. ^{{harvnb|Knapp|2001}} Equation 2.4.
116. ^{{harvnb|Knapp|2001}}
117. ^{{harvnb|Knapp|2001|loc=Section 2.3.}}
118. ^{{harvnb|Rossmann|2002|loc=Proposition 10, paragraph 6.3.}} This is easiest proved using character theory.
119. ^{{harvnb|Hall|2015|loc=Theorems 9.4–5.}}
120. ^{{harvnb|Weinberg|2002|loc=Chapter 5.}}
121. ^{{harvnb|Hall|2015|loc= Theorem 10.18.}}
122. ^{{harvnb|Hall|2003|p=235.}}
123. ^See any text on basic group theory.
124. ^Any discrete normal subgroup of a path connected group {{math|G}} is contained in the center {{math|Z}} of {{math|G}}.{{Paragraph break}}{{harvnb|Hall|2015|loc=Exercise 11, chapter 1.}}
125. ^A semisimple Lie group does not have any non-discrete normal abelian subgroups. This can be taken as the definition of semisimplicity.
126. ^A simple group does not have any non-discrete normal subgroups.
127. ^{{harvnb|Rossmann|2002}} Propositions 3 and 6 paragraph 2.5.
128. ^{{harvnb|Hall|2003}} See exercise 1, Chapter 6.
129. ^By contrast, there is a trick, also called Weyl's unitarian trick, but unrelated to the unitarian trick of above showing that all finite-dimensional representations are, or can be made, unitary. If {{math|(Π, V)}} is a finite-dimensional representation of a compact Lie group {{mvar|G}} and if {{math|(·, ·)}} is any inner product on {{mvar|V}}, define a new inner product {{math|(·, ·)Π}} by {{math|(x, y)Π {{=}} ∫G(Π(g)x, Π(g)y dμ(g)}}, where {{mvar|μ}} is Haar measure on {{mvar|G}}. Then {{math|Π}} is unitary with respect to {{math|(·, ·)Π}}. See {{harvtxt|Hall|2015|loc=Theorem 4.28.}}{{Paragraph break}}Another consequence is that every compact Lie group has the complete reducibility property, meaning that all its finite-dimensional representations decompose as a direct sum of irreducible representations. {{harvtxt|Hall|2015|loc=Definition 4.24., Theorem 4.28.}}{{Paragraph break}}It is also true that there are no infinite-dimensional irreducible unitary representations of compact Lie groups, stated, but not proved in {{harvtxt|Greiner|Müller|1994|loc=Section 15.2.}}.
130. ^{{harvnb|Bekaert|Boulanger|2006}} p.4.
131. ^{{harvnb|Hall|2003}} Proposition 1.20.
132. ^{{harvnb|Lee|2003|loc=Theorem 8.30.}}
133. ^{{harvnb|Lee|2003}} Lemma A.17 (c). Closed subsets of compact sets are compact.
134. ^{{harvnb|Lee|2003}} Lemma A.17 (a). If {{math|f : X → Y}} is continuous, {{mvar|X}} is compact, then {{math|f(X)}} is compact.
135. ^The non-unitarity is a vital ingredient in the proof of the Coleman–Mandula theorem, which has the implication that, contrary to in non-relativistic theories, there can exist no ordinary symmetry relating particles of different spin. See {{harvtxt|Weinberg|2000|loch=Chapter 24.}}
136. ^{{harvnb|Weinberg|2002|loc=Section 5.6, p. 231.}}
137. ^{{harvnb|Weinberg|2002|loc=Section 5.6.}}
138. ^{{harvnb|Weinberg|2002|p=231.}}
139. ^{{harvnb|Weinberg|2002|loc=Sections 2.5, 5.7.}}
140. ^{{harvnb|Tung|1985|loc=Section 10.5.}}
141. ^{{harvnb|Weinberg|2002}} This is outlined (very briefly) on page 232, hardly more than a footnote.
142. ^{{harvnb|Hall|2003|loc=Proposition 7.39.}}
143. ^This is one of the conclusions of Cartan's theorem, the theorem of the highest weight.{{Paragraph break}}{{harvtxt|Hall|2015|loc=Theorems 9.4–5.}}
144. ^1 {{harvnb|Hall|2003|loc=Theorem 7.40.}}
145. ^{{harvnb|Hall|2003|loc=Section 6.6.}}
146. ^{{harvnb|Hall|2015|loc=Section 8.2}} The root system is the union of two copies of {{math|A1}}, where each copy resides in its own dimensions in the embedding vector space.
147. ^{{harvnb|Rossmann|2002}} This definition is equivalent to the definition in terms of the connected Lie group whose Lie algebra is the Lie algebra of the root system under consideration.
148. ^{{harvnb|Hall|2003|loc=Second item in proposition 4.5.}}
149. ^{{harvnb|Hall|2003|p=219.}}
150. ^{{harvnb|Rossmann|2002|loc=Exercise 3 in paragraph 6.5.}}
151. ^{{harvnb|Hall|2003}} See appendix D.3
152. ^{{harvnb|Weinberg|2002|loc=Equation 5.4.8.}}
153. ^1 {{harvnb|Weinberg|2002|loc=Section 5.4.}}
154. ^{{harvnb|Weinberg|2002|pp=215–216.}}
155. ^{{harvnb|Weinberg|2002|loc=Equation 5.4.6.}}
156. ^{{harvnb|Weinberg|2002}} Section 5.4.
157. ^{{harvnb|Weinberg|2002|loc=Section 5.7, pp. 232–233.}}
158. ^{{harvnb|Weinberg|2002|loc=Section 5.7, p. 233.}}
159. ^{{harvnb|Weinberg|2002}} Equation 2.6.5.
160. ^{{harvnb|Weinberg|2002}} Equation following 2.6.6.
161. ^{{harvnb|Weinberg|2002|loc=Section 2.6.}}
162. ^For a detailed discussion of the spin 0, {{sfrac|1|2}} and 1 cases, see {{harvnb|Greiner|Reinhardt|1996}}.
163. ^{{harvnb|Weinberg|2002|loc=Chapter 3.}}
164. ^{{harvnb|Rossmann|2002}} See section 6.1 for more examples, both finite-dimensional and infinite-dimensional.
165. ^{{harvnb|Gelfand|Minlos|Shapiro|1963}}
166. ^{{harvnb|Churchill|Brown|2014|loc=Chapter 8 pp. 307–310.}}
167. ^{{cite journal|ref=harv|last1=Gonzalez|first1=P. A.|last2=Vasquez|first2=Y.|title=Dirac Quasinormal Modes of New Type Black Holes in New Massive Gravity|year=2014|journal= Eur. Phys. J. C |issn=1434-6044|volume=74:2969|issue=7|arxiv=1404.5371|doi=10.1140/epjc/s10052-014-2969-1|page=3|bibcode=2014EPJC...74.2969G}}
168. ^{{harvnb|Abramowitz|Stegun|1965|loc=Equation 15.6.5.}}
169. ^{{harvnb|Simmons|1972|loc=Sections 30, 31.}}
170. ^See {{harvtxt|Simmons|1972|loc=Section 30.}} for precise conditions under which two Frobenius method yields two linearly independent solutions. If the exponents do not differ by an integer, this is always the case.
171. ^{{harvnb|Simmons|1972|loc=Sections 30.}}
172. ^{{harvnb|Simmons|1972|loc=Section 31.}}
173. ^{{harvnb|Simmons|1972|loc=Equation 11 in appendix E, chapter 5.}}
174. ^{{harvnb|Langlands|1985|p=205.}}
175. ^{{harvnb|Varadarajan|1989|loc=Sections 3.1. 4.1.}}
176. ^{{harvnb|Langlands|1985|p=203.}}
177. ^"This is as close as one comes to the source of the theory of infinite-dimensional representations of semisimple and reductive groups...", {{harvtxt|Langlands|1985|p=204.}}, referring to an introductory passage in Dirac's 1945 paper.
178. ^{{harvnb|Varadarajan|1989|loc=Section 4.1.}}
179. ^{{harvnb|Gelfand|Graev|Pyatetskii-Shapiro|1969}}
180. ^{{harvnb|Knapp|2001|loc=Chapter II.}}
181. ^1 2 {{harvnb|Harish-Chandra|1947}}
182. ^1 {{harvnb|Taylor|1986}}
183. ^{{harvnb|Knapp|2001}} Chapter 2. Equation 2.12.
184. ^{{harvnb|Bargmann|1947}}
185. ^{{harvnb|Gelfand|Graev|1953}}
186. ^{{harvnb|Gelfand|Naimark|1947}}
187. ^{{harvnb|Takahashi|1963|page=343.}}
188. ^Note that for a Hilbert space {{mvar|H}}, {{math|HS(H)}} may be identified canonically with the Hilbert space tensor product of {{mvar|H}} and its conjugate space.
189. ^{{harvnb|Knapp|2001|loc=Equation 2.24.}}
190. ^{{harvnb|Folland|2015|loc=Section 3.1.}}
191. ^{{harvnb|Folland|2015|loc=Theorem 5.2.}}
192. ^{{harvnb|Tung|1985|loc=Section 10.3.3.}}
193. ^If finite-dimensionality is demanded, the results is the {{math|(m, n)}} representations, see {{harvtxt|Tung|1985|loc=Problem 10.8.}} If neither is demanded, then a broader classification of all irreducible representations is obtained, including the finite-dimensional and the unitary ones. This approach is taken in {{harvtxt|Harish-Chandra|1947}}.
194. ^{{harvnb|Harish-Chandra|1947|loc=Footnote p. 374.}}
195. ^{{harvnb|Tung|1985|loc=Equations 7.3–13, 7.3–14.}}
196. ^{{harvnb|Harish-Chandra|1947|loc=Equation 8.}}
197. ^{{harvnb|Hall|2015|loc=Proposition C.7.}}
198. ^{{harvnb|Hall|2015|loc=Appendix C.2.}}
199. ^{{harvnb|Tung|1985|loc=Step II section 10.2.}}
200. ^{{harvnb|Tung|1985|loc=Equations 10.3–5. Tung's notation for Clebsch–Gordan coefficients differ from the one used here.}}
201. ^{{harvnb|Tung|1985|loc=Equation VII-3.}}
202. ^{{harvnb|Tung|1985|loc=Equations 10.3–5, 7, 8.}}
203. ^{{harvnb|Tung|1985|loc=Equation VII-9.}}
204. ^{{harvnb|Tung|1985|loc=Equations VII-10, 11.}}
205. ^{{harvnb|Tung|1985|loc=Equations VII-12.}}
206. ^{{harvnb|Tung|1985|loc=Equations VII-13.}}
207. ^{{harvnb|Weinberg|2002|loc=Equation 2.4.12.}}
208. ^{{harvnb|Weinberg|2002|loc=Equations 2.4.18–2.4.20.}}
209. ^{{harvnb|Weinberg|2002|loc=Equations 5.4.19, 5.4.20.}}
Notes
{{reflist|30em}}Freely available online references
- {{cite arXiv|ref=harv|last = Bekaert|last2 = Boulanger|first = X.|first2 = N.|year = 2006|title = The unitary representations of the Poincare group in any spacetime dimension|eprint = hep-th/0611263}} Expanded version of the lectures presented at the second Modave summer school in mathematical physics (Belgium, August 2006).
- {{citation|last = Curtright|first = T L |last2=Fairlie|first2= D B|last3=Zachos|first3 = C K|year = 2014|title = A compact formula for rotations as spin matrix polynomials| journal =SIGMA| volume=10| page=084|doi=10.3842/SIGMA.2014.084|authorlink1=Thomas Curtright|authorlink2=David Fairlie|authorlink3=Cosmas Zachos|arxiv = 1402.3541 |bibcode = 2014SIGMA..10..084C }} Group elements of SU(2) are expressed in closed form as finite polynomials of the Lie algebra generators, for all definite spin representations of the rotation group.
References
- {{cite book|ref=harv|last1=Abramowitz|first1=M.|authorlink1=Milton Abramowitz|last2=Stegun|first2=I. A.|authorlink2=Irene Stegun|title=Handbook of Mathematical Functions: with Formulas, Graphs, and Mathematical Tables|year=1965|isbn=978-0486612720|publisher=Dover Publications|location=New York|series=Dover Books on Mathematics|url=https://books.google.com/books?id=MtU8uP7XMvoC&pg=PR9}}
- {{citation|doi=10.2307/1969129|first=V.|last= Bargmann|title=Irreducible unitary representations of the Lorenz group|journal=Ann. of Math.|volume= 48|issue=3| year=1947|pages=568–640|postscript=|jstor=1969129|authorlink=Valentine Bargmann}} (the representation theory of SO(2,1) and SL(2, R); the second part on SO(3; 1) and SL(2, C), described in the introduction, was never published).
- {{citation|last=Bargmann|first=V.|last2=Wigner|first2=E. P.|title=Group theoretical discussion of relativistic wave equations|year=1948|journal=Proc. Natl. Acad. Sci. USA|volume=34|pages=211–23|url=http://www.pnas.org/cgi/content/citation/34/5/211|issue=5|doi= 10.1073/pnas.34.5.211|bibcode=1948PNAS...34..211B|pmid=16578292|pmc=1079095}}
- {{cite book|ref=harv|last=Bourbaki|first=N.|authorlink=Nicolas Bourbaki|title=Lie Groups and Lie Algebras: Chapters 1-3|year=1998|isbn=978-3-540-64242-8|publisher=Springer|url=https://books.google.com/books?id=brSYF_rB2ZcC}}
- {{citation|last1=Brauer|first1=R.|last2=Weyl|first2=H.|title=Spinors in n dimensions|journal=Amer. J. Math.|volume=57|issue=2|year=1935|pages=425–449|authorlink1=Richard Brauer|doi=10.2307/2371218|jstor=2371218}}
- {{cite book|ref=harv|last1=Bäuerle|first1=G.G.A|last2=de Kerf|first2=E.A.|title=Finite and infinite dimensional Lie algebras and their application in physics|year=1990|series=Studies in mathematical physics|volume=1|editor1=A. van Groesen|editor2=E.M. de Jager|publisher=North-Holland|isbn=978-0-444-88776-4}}
- {{cite book|ref=harv|last1=Bäuerle|first1=G.G.A|last2=de Kerf|first2=E.A.|last3=ten Kroode|first3=A.P.E.|title=Finite and infinite dimensional Lie algebras and their application in physics|year=1997|series=Studies in mathematical physics|volume=7|editor1=A. van Groesen|editor2=E.M. de Jager|publisher=North-Holland|isbn=978-0-444-82836-1|url=http://www.sciencedirect.com/science/bookseries/09258582|via=ScienceDirect|subscription=yes}}
- {{citation|last=Cartan|first=Élie|year=1913|title=Les groupes projectifs qui ne laissant invariante aucun multiplicité plane|journal=Bull. Soc. Math. Fr.|volume=41|pages=53–96|authorlink=Élie Cartan|language=French|postscript=|doi=10.24033/bsmf.916}}
- {{cite book|ref=harv|last1=Churchill|first1=R. V.|authorlink1=Ruel Vance Churchill|last2=Brown|first2=J. W.|title=Complex Variables and Applications|edition=9th|orig-year=1948|year=2014|isbn=978-0073-383-170|publisher=McGraw–Hill|location=New York}}
- {{cite journal|ref=harv|last=Coleman|first=A. J.|title=The Greatest Mathematical Paper of All Time|year=1989|journal=The Mathematical Intelligencer|volume=11|issue=3|pages=29–38|doi=10.1007/BF03025189|issn=0343-6993}}
- {{cite journal|first=R. H.|last=Dalitz|first2=Rudolf|last2=Peierls|journal=Biogr. Mem. Fellows R. Soc.|year=1986|volume=32|pages=138–185|ref=harv|title=Paul Adrien Maurice Dirac. 8 August 1902–20 October 1984|doi=10.1098/rsbm.1986.0006}}
- {{cite journal|ref=harv|last1=Delbourgo|first1=R.|authorlink1=Robert Delbourgo|last2=Salam|first2=A.|authorlink2=Abdus Salam|last3=Strathdee|first3=J.|title=Harmonic analysis in terms of the homogeneous Lorentz group|journal=Physics Letters B|volume=25|issue=3|year=1967|doi=10.1016/0370-2693(67)90050-0|pages=230–32|via=ScienceDirect|subscription=yes|url=http://www.sciencedirect.com/science/article/pii/0370269367900500|bibcode=1967PhLB...25..230D}}
- {{citation|doi=10.1098/rspa.1928.0023|title=The Quantum Theory of the Electron|year=1928|last1=Dirac|first1=P. A. M.|journal=Proc. Roy. Soc. A|volume=117|issue=778|pages=610–624|bibcode = 1928RSPSA.117..610D|authorlink=Paul Dirac}} (free access)
- {{citation|last=Dirac|first=P. A. M.|title=Relativistic wave equations|year=1936|authorlink=Paul Dirac|journal=Proc. Roy. Soc. A|volume=155|pages=447–459|doi=10.1098/rspa.1936.0111|issue=886|bibcode=1936RSPSA.155..447D}}
- {{citation|last=Dirac|first=P. A. M.|title=Unitary representations of the Lorentz group|year=1945|authorlink=Paul Dirac|journal=Proc. Roy. Soc. A|volume=183|pages=284–295|doi=10.1098/rspa.1945.0003|issue=994|bibcode=1945RSPSA.183..284D}}
- {{citation|first=J.|last=Dixmier|authorlink=Jacques Dixmier|first2=P.|last2=Malliavin|authorlink2=Paul Malliavin|title=Factorisations de fonctions et de vecteurs indéfiniment différentiables|journal= Bull. Sc. Math.|volume =102 |year=1978|pages= 305–330|language=French|postscript=}}
- {{citation|last=Fierz|first=M.|year=1939|journal=Helv. Phys. Acta|volume=12|issue=1|pages=3–37|authorlink=Markus Fierz|language=German|title=Über die relativistische theorie Kräftefreier teilchen mit beliebigem spin|doi=10.5169/seals-110930|postscript=(pdf download available)}}
- {{citation|last=Fierz|first=M.|last2=Pauli|first2=W.|year=1939|journal=Proc. Roy. Soc. A|volume=173|issue=953|pages=211–232|bibcode=1939RSPSA.173..211F|authorlink=Markus Fierz|authorlink2=Wolfgang Pauli|title=On relativistic wave equations for particles of arbitrary spin in an electromagnetic field|doi=10.1098/rspa.1939.0140}}
- {{cite book|ref=harv|first=G.|last=Folland|authorlink=Gerald Folland|title=A Course in Abstract Harmonic Analysis|edition=2nd|year=2015|publisher=CRC Press|isbn=978-1498727136}}
- {{cite book|ref=harv|last1=Fulton|first1=W.|authorlink1=William Fulton (mathematician)|last2=Harris|first2=J.|authorlink2=Joe Harris (mathematician)|year=1991|title=Representation theory. A first course|series=Graduate Texts in Mathematics|volume=129|location=New York|publisher=Springer-Verlag|isbn=978-0-387-97495-8|mr=1153249}}
- {{Citation|first1=I. M.|last1=Gelfand|first2=M. I.|last2=Graev|title=On a general method of decomposition of the regular representation of a Lie group into irreducible representations|journal=Doklady Akademii Nauk SSSR|volume= 92|year=1953| pages=221–224|postscript=}}
- {{citation|last1=Gelfand|first1=I. M.|last2= Graev|first2= M. I.|last3= Vilenkin|first3= N. Ya.|title=Generalized functions. Vol. 5: Integral geometry and representation theory|translator=Eugene Saletan|publisher= Academic Press|year=1966|chapter=Harmonic analysis on the group of complex unimodular matrices in two dimensions|pages=202–267|isbn=978-1-4832-2975-1}}
- {{citation|last=Gelfand|first= I. M.|last2=Graev|first2= M. I.|last3= Pyatetskii-Shapiro|first3= I. I.|title=Representation theory and automorphic functions|publisher= Academic Press|year=1969|isbn=978-0-12-279506-0|authorlink3=Ilya Piatetski-Shapiro}}
- {{citation|first1=I.M.|last1=Gelfand|first2=R.A.|last2=Minlos|first3=Z. Ya.|last3=Shapiro|title=Representations of the Rotation and Lorentz Groups and their Applications|publisher=Pergamon Press|location=New York|year=1963|authorlink1=Israel Gelfand|authorlink2=Robert Adol'fovich Minlos}}
- {{citation|first=I. M.|last=Gelfand|authorlink=I. M. Gelfand|first2=M. A.|last2=Naimark|authorlink2=Mark Naimark|title=Unitary representations of the Lorentz group|journal=Izvestiya Akad. Nauk SSSR. Ser. Mat.|volume= 11|issue=5|year=1947|pages=411–504|language=Russian|url=http://www.mathnet.ru/links/716f895de8c01ce39ce0a83666f73303/im3007.pdf|access-date=2014-12-15|postscript= (Pdf from Math.net.ru)}}
- {{cite book|ref=harv|title=Biographical Memoirs|publisher=National Academy Press|authorlink=Sandy Green (mathematician)|isbn=978-0309062954|pages=70–95|series=Biographical Memoirs|volume=75|year=1998|chapter=Richard Dagobert Brauer|chapter-url=http://www.nasonline.org/publications/biographical-memoirs/memoir-pdfs/brauer-richard-d.pdf|last=Green|first=J. A.}}
- {{cite book|ref=harv|last1=Greiner|first=W.|last2=Müller|first2=B.|title=Quantum Mechanics: Symmetries|year=1994|edition=2nd|isbn=978-3540580805|publisher=Springer}}
- {{citation|last=Greiner|first=W.|authorlink1=Walter Greiner|last2=Reinhardt|first2=J.|year=1996|title=Field Quantization|publisher=Springer|isbn=978-3-540-59179-5}}
- {{citation|doi=10.1098/rspa.1947.0047|last=Harish-Chandra|authorlink=Harish-Chandra|title=Infinite irreducible representations of the Lorentz group|journal=Proc. Roy. Soc. A|volume= 189|year=1947|issue=1018|pages=372–401|postscript=|bibcode = 1947RSPSA.189..372H }}
- {{citation|doi=10.1073/pnas.37.12.813|last=Harish-Chandra|title=Plancherel formula for complex semi-simple Lie groups|journal=Proc. Natl. Acad. Sci. U.S.A.|volume= 37|year=1951|issue=12|pages=813–818|postscript=|bibcode = 1951PNAS...37..813H |pmc=1063477}}
- {{citation|year=2003|first=Brian C.|last=Hall|title=Lie Groups, Lie Algebras, and Representations: An Elementary Introduction|publisher=Springer|isbn= 978-0-387-40122-5|series=Graduate Texts in Mathematics|volume=222|edition=1st}}
- {{Citation| last=Hall|first=Brian C.|title=Lie groups, Lie algebras, and Representations: An Elementary Entroduction|edition=2nd|series=Graduate Texts in Mathematics|volume=222|publisher=Springer|year=2015|isbn=978-3319134666|doi=10.1007/978-3-319-13467-3|issn=0072-5285}}
- {{citation|last=Helgason|first= S.|title=Lie groups and symmetric spaces|series=Battelle Rencontres|year=1968|pages= 1–71|publisher= Benjamin|authorlink=Sigurdur Helgason (mathematician)|postscript=}} (a general introduction for physicists)
- {{citation|last=Helgason|first= S.|title=Groups and geometric analysis. Integral geometry, invariant differential operators, and spherical functions (corrected reprint of the 1984 original)|series=Mathematical Surveys and Monographs|volume=83|publisher= American Mathematical Society|year= 2000|isbn= 978-0-8218-2673-7|postscript=}}
- {{citation|last2=Lang|first2=S.|authorlink2=Serge Lang|last=Jorgenson|first=J.|title=The heat kernel and theta inversion on SL(2,C)|
series=Springer Monographs in Mathematics|publisher= Springer|year=2008|isbn=978-0-387-38031-5|postscript=}}
- {{citation|last=Killing|year=1888|first=Wilhelm|title=Die Zusammensetzung der stetigen/endlichen Transformationsgruppen|journal=Mathematische Annalen|volume=31|issue=2 (June)|pages=252–290|authorlink=Wilhelm Killing|postscript=|doi=10.1007/bf01211904|language=German}}
- {{cite book|ref=harv|last=Kirillov|first=A.|title=An Introduction to Lie Groups and Lie Algebras|year=2008|isbn=978-0521889698|publisher=Cambridge University Press|series=Cambridge Studies in Advanced Mathematics|volume=113|url=https://books.google.com/?id=-Z3cDQAAQBAJ&printsec=frontcover&dq=Introduction+to+Lie+groups+and+Lie+algebras#v=onepage&q=Introduction%20to%20Lie%20groups%20and%20Lie%20algebras&f=false}}
- {{cite book|ref=harv|year=1999|last=Klauder|first=J. R.|chapter-url=http://www.nasonline.org/publications/biographical-memoirs/memoir-pdfs/bargmann-valentine.pdf|chapter=Valentine Bargmann|title=Biographical Memoirs|volume=76|pages=37–50|publisher=National Academy Press|isbn=978-0-309-06434-7|authorlink=John R. Klauder|series=Biographical Memoirs}}
- {{citation|first=Anthony W.|last= Knapp| title=Representation theory of semisimple groups. An overview based on examples. |series=Princeton Landmarks in Mathematics|publisher=Princeton University Press|year=2001|isbn=978-0-691-09089-4|authorlink=Anthony W. Knapp|postscript=}} (elementary treatment for SL(2,C))
- {{cite journal|ref=harv|first=R. P.|last=Langlands|authorlink=Robert Langlands|title=Harish-Chandra|journal=Biogr. Mems Fell.|year=1985|volume=31|pages=198–225|doi=10.1098/rsbm.1985.0008|url=http://rsbm.royalsocietypublishing.org/content/31/198}}
- {{citation|last = Lee|first = J. M.|title=Introduction to Smooth manifolds|year=2003|series=Springer Graduate Texts in Mathematics|isbn=978-0-387-95448-6|volume=218|postscript=}}
- {{citation|last=Lie|first=Sophus|title=Theorie der Transformationsgruppen I(1888), II(1890), III(1893)|year=1888|authorlink=Sophus Lie|postscript=|language=German}}
- {{Citation|first=Charles W.|last=Misner|authorlink=Charles W. Misner|first2=Kip. S.|last2=Thorne|author2-link=Kip Thorne|first3=John A.|last3=Wheeler|author3-link=John A. Wheeler|title=Gravitation|publisher= W. H. Freeman|date=1973|isbn=978-0-7167-0344-0|title-link=Gravitation (book)}}
- {{citation|first=M.A.|last=Naimark|title=Linear representations of the Lorentz group (translated from the Russian original by Ann Swinfen and O. J. Marstrand) |publisher=Macmillan|year= 1964|authorlink=Mark Naimark|postscript=}}
- {{citation|last=Rossmann|first= Wulf|title=Lie Groups – An Introduction Through Linear Groups|publisher=Oxford Science Publications|year=2002|series=Oxford Graduate Texts in Mathematics|isbn=0 19 859683 9|postscript=}}
- {{citation|last=Rühl|first= W.|title=The Lorentz group and harmonic analysis|publisher=Benjamin|year= 1970|postscript=}} (a detailed account for physicists)
- {{cite book|ref=harv|first=G. F.|last=Simmons|title=Differential Equations with Applications and historical Notes|year=1972|edition=T M H|isbn=978-0-07-099572-7|publisher=Tata McGra–Hill Publishing Company Ltd|location=New Dheli}}
- {{citation|last=Stein|first= Elias M.|authorlink=Elias M. Stein|title=Analytic continuation of group representations|journal=Advances in Mathematics |volume=4|issue= 2|year= 1970 |pages=172–207|url=http://www.sciencedirect.com/science/article/pii/0001870870900228|doi=10.1016/0001-8708(70)90022-8}} (James K. Whittemore Lectures in Mathematics given at Yale University, 1967)
- {{citation|last=Takahashi|first= R.|title=Sur les représentations unitaires des groupes de Lorentz généralisés|journal=Bull. Soc. Math. France|volume= 91| year=1963|pages= 289–433|language=French|postscript=|doi= 10.24033/bsmf.1598}}
- {{citation|last=Taylor|first=M. E.|authorlink=Michael E. Taylor|title=Noncommutative harmonic analysis|series=Mathematical Surveys and Monographs|volume= 22|publisher= American Mathematical Society|year=1986|isbn=978-0-8218-1523-6|postscript=}}, Chapter 9, SL(2, C) and more general Lorentz groups
- {{cite book|ref=harv|title=Group Theory in Physics|edition=1st|location=New Jersey·London·Singapore·Hong Kong|year=1985|isbn=978-9971966577|publisher=World Scientific|last=Tung|first=Wu-Ki}}
- {{cite book|ref=harv|first=V. S.|last=Varadarajan|authorlink=Veeravalli S. Varadarajan|title=An Introduction to Harmonic Analysis on Semisimple Lie Groups|year=1989|publisher=Cambridge University Press|isbn=978-0521663625}}
- {{citation|last=Weinberg|first=S.|year=2002|orig-year=1995|title=Foundations|series=The Quantum Theory of Fields|volume=1|isbn=978-0-521-55001-7|authorlink=Steven Weinberg|location=Cambridge|publisher=Cambridge University Press}}
- {{cite book|ref=harv|last=Weinberg|first=S.|title=Supersymmetry|year=2000|edition=1st|series=The Quantum Theory of Fields|volume=3|publisher=Cambridge University Press|location=Cambridge|isbn=978-0521670555}}
- {{Citation | last1=Weyl | first1=H. | author1-link=Hermann Weyl | title=The Classical Groups. Their Invariants and Representations | url=https://books.google.com/books?isbn=0691057567 | publisher=Princeton University Press | isbn=978-0-691-05756-9 | year=1939 | mr=0000255}}
- {{Citation|last=Weyl|first=H.|year=1931|title=The Theory of Groups and Quantum Mechanics|publisher=Dover|isbn=978-0-486-60269-1}}
- {{citation|first=E. P.|last=Wigner|authorlink=Eugene Wigner|title=On unitary representations of the inhomogeneous Lorentz group|journal=Annals of Mathematics|issue=1|volume=40|pages=149–204|year=1939|doi=10.2307/1968551|mr=1503456|bibcode=1939AnMat..40..922E|jstor=1968551}}.
- {{cite book|ref=harv|last=Zwiebach|first=B.|authorlink=Barton Zwiebach|title=A First Course in String Theory|year=2004|publisher=Cambridge University Press|isbn=0 521 83143 1}}
- Lux perpetua (novel)
- Lux Radio Theater
- LUX* Resorts & Hotels
- LuxR-type DNA-binding HTH domain
- LUXS
- Luxspace
- LuxSpace
- Lux Style Award
- Luxted
- Luxton lake
- Luxton Lake
- Luxton lake (Nova Scotia)
- Luxton Lake (Nova Scotia)
- Luxtorpeda (band)
- Luxulyan Quarry
- Luxumburg
- Lu Xun Academy
- Lu Xun Academy of Fine Arts
- Lu Xun Museum
- Luxurians
- Luxuriant ringstalk
- Luxuria (vice)
- Luxuris Celje
- Luxury (album)
- Luxury and packaging