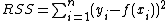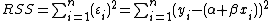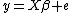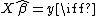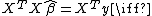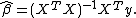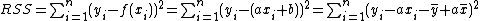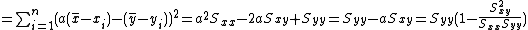- One explanatory variable
- Matrix expression for the OLS residual sum of squares
- Relation with Pearson's product-moment correlation
- See also
- References
In statistics, the residual sum of squares (RSS), also known as the sum of squared residuals (SSR) or the sum of squared errors of prediction (SSE), is the sum of the squares of residuals (deviations predicted from actual empirical values of data). It is a measure of the discrepancy between the data and an estimation model. A small RSS indicates a tight fit of the model to the data. It is used as an optimality criterion in parameter selection and model selection.
In general, total sum of squares = explained sum of squares + residual sum of squares. For a proof of this in the multivariate ordinary least squares (OLS) case, see partitioning in the general OLS model.
One explanatory variable
In a model with a single explanatory variable, RSS is given by:
where yi is the i th value of the variable to be predicted, xi is the i th value of the explanatory variable, and  is the predicted value of yi (also termed
is the predicted value of yi (also termed 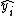 ).
).
In a standard linear simple regression model, 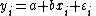 , where a and b are coefficients, y and x are the regressand and the regressor, respectively, and ε is the error term. The sum of squares of residuals is the sum of squares of estimates of εi; that is
, where a and b are coefficients, y and x are the regressand and the regressor, respectively, and ε is the error term. The sum of squares of residuals is the sum of squares of estimates of εi; that is
where  is the estimated value of the constant term
is the estimated value of the constant term  and
and 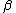 is the estimated value of the slope coefficient b.
is the estimated value of the slope coefficient b.
Matrix expression for the OLS residual sum of squares
The general regression model with 'n' observations and 'k' explanators, the first of which is a constant unit vector whose coefficient is the regression intercept, is
where y is an n × 1 vector of dependent variable observations, each column of the n × k matrix X is a vector of observations on one of the k explanators, 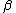 is a k × 1 vector of true coefficients, and e is an n× 1 vector of the true underlying errors. The ordinary least squares estimator for
is a k × 1 vector of true coefficients, and e is an n× 1 vector of the true underlying errors. The ordinary least squares estimator for 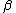 is
is
The residual vector  =
= 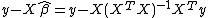 , so the residual sum of squares is:
, so the residual sum of squares is:
{{anchor|Norm of residuals}}(equivalent to the square of the norm of residuals); in full:,
,
where H is the hat matrix, or the projection matrix in linear regression.
Relation with Pearson's product-moment correlation
The least-squares regression line is given by
,
where 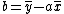 and
and 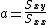 , where
, where 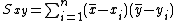 and
and 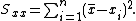
Therefore,
where 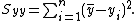
The Pearson product-moment correlation is given by 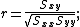 therefore,
therefore, 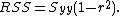
See also
- Sum of squares (statistics)
- Squared deviations
- Errors and residuals in statistics
- Lack-of-fit sum of squares
- Degrees of freedom (statistics)#Sum of squares and degrees of freedom
- Chi-squared distribution#Applications
- Mean squared error
References
- {{cite book
|title = Applied Regression Analysis
|edition = 3rd
|last1= Draper |first1=N.R. |last2=Smith |first2=H.
|publisher = John Wiley
|year = 1998
|isbn = 0-471-17082-8}}
- Quintuple product identity
- Quintus
- Quintus Aelius Tubero (Stoic)
- Quintus Aemilius Lepidus
- Quintus Anicius Faustus Paulinus
- Quintus Arrius (Ben-Hur)
- Quintus Arrius (disambiguation)
- Quintus Arrius (praetor 73 BC)
- Quintus Aulus Pompeius
- Quintus Cervidius Scaevola
- Quintus Cloelius Siculus
- Quintus Fabius Maximus (consul 213 BC)
- Quintus Fabius Maximus (disambiguation)
- Quintus Fabius Maximus Servilianus (consul 142 BC)
- Quintus Fabius Maximus The Younger
- Quintus Fabius Maximus Verucosus
- Quintus Fabius Vibulanus (consul 485 and 482 BC)
- Quintus Fabricius
- Quintus Hedius Lollianus Plautius Avitus
- Quintus Hedius Rufus Lollianus Gentianus
- Quintus Hortensius (consul designate 108 BC)
- Quintus Laronius
- Quintus Marcius Barea Sura
- Quintus Marcius Crispus
- Quintus Marcius Rex